Next: Tisserand Criterion
Up: The Three-Body Problem
Previous: Circular Restricted Three-Body Problem
Jacobi Integral
Consider the function
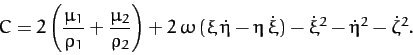 |
(1039) |
The time derivative of this function is
written
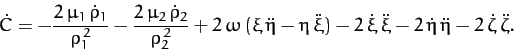 |
(1040) |
Moreover, it follows, from Equations (1032)-(1033) and (1037)-(1038),
that
Combining Equations (1034)-(1036) with the above three expressions, we obtain (after considerable
algebra)
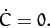 |
(1043) |
In other words, the function 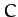 --which is usually referred to as the Jacobi integral--is a constant of the motion.
--which is usually referred to as the Jacobi integral--is a constant of the motion.
Now, we can rearrange Equation (1039) to give
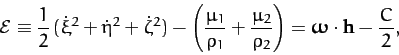 |
(1044) |
where 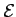 is the energy (per unit mass) of mass
is the energy (per unit mass) of mass 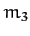 ,
,
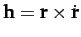 its angular momentum
(per unit mass), and
its angular momentum
(per unit mass), and
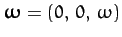 the orbital angular velocity of the other two masses.
Note, however, that
the orbital angular velocity of the other two masses.
Note, however, that 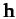 is not a constant of the motion. Hence,
is not a constant of the motion. Hence, 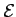 is not
a constant of the motion either. In fact, the Jacobi integral is the only constant of the
motion in the circular restricted three-body problem. Incidentally, the energy
of mass
is not
a constant of the motion either. In fact, the Jacobi integral is the only constant of the
motion in the circular restricted three-body problem. Incidentally, the energy
of mass 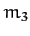 is not a conserved quantity because the other two masses in the system
are moving.
is not a conserved quantity because the other two masses in the system
are moving.



Next: Tisserand Criterion
Up: The Three-Body Problem
Previous: Circular Restricted Three-Body Problem
Richard Fitzpatrick
2011-03-31