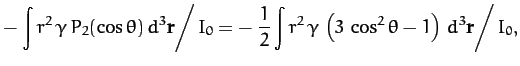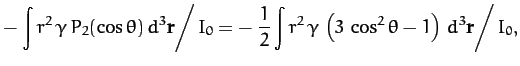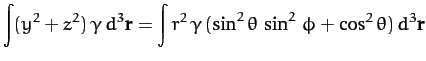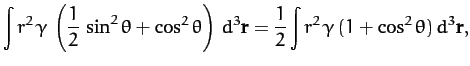Next: Tidal Elongation
Up: Gravitational Potential Theory
Previous: Rotational Flattening
McCullough's Formula
According to Equations (903) and (908), if the Earth
is modeled as spheroid of uniform density 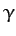 then its ellipticity
is given by
then its ellipticity
is given by
where the integral is over the whole volume of the Earth, and
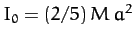 would be the Earth's moment of inertia were it
exactly spherical. Now, the Earth's moment of inertia about its
axis of rotation is given by
would be the Earth's moment of inertia were it
exactly spherical. Now, the Earth's moment of inertia about its
axis of rotation is given by
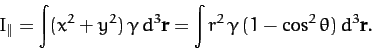 |
(923) |
Here, use has been made of Equations (869)-(871). Likewise,
the Earth's moment of inertia about an axis perpendicular to its
axis of rotation (and passing through the Earth's center) is
since the average of  is
is 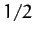 for an axisymmetric mass distribution. It follows from the above three equations that
for an axisymmetric mass distribution. It follows from the above three equations that
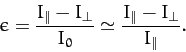 |
(925) |
This result, which is known as McCullough's formula, demonstrates
that the Earth's ellipticity is directly related to the difference between
its principle moments of inertia. It turns out that McCullough's formula
holds for any axially symmetric mass distribution, and not
just a spheroidal distribution with uniform density. Finally, McCullough's
formula can be combined with Equation (909) to give
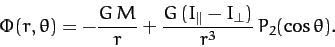 |
(926) |
This is the general expression for the gravitational potential generated outside
an axially symmetric mass distribution. The first term on the right-hand
side is the monopole gravitational field which would be generated
if all of the mass in the distribution were concentrated at its center of mass,
whereas the second term is the quadrupole field generated by any deviation from spherical symmetry in the distribution.



Next: Tidal Elongation
Up: Gravitational Potential Theory
Previous: Rotational Flattening
Richard Fitzpatrick
2011-03-31