


Next: Exercises
Up: Lagrangian Dynamics
Previous: Generalized Momenta
Consider a pendulum consisting of a compact mass 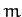 on the end of light
inextensible string of length
on the end of light
inextensible string of length 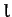 . Suppose that the mass is free to move
in any direction (as long as the string remains taut). Let the
fixed end of the string be located at the origin of our coordinate system.
We can define Cartesian coordinates, (
. Suppose that the mass is free to move
in any direction (as long as the string remains taut). Let the
fixed end of the string be located at the origin of our coordinate system.
We can define Cartesian coordinates, ( ,
, 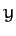 ,
, 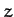 ), such that
the
), such that
the 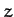 -axis points vertically upward. We can also define spherical
coordinates, (
-axis points vertically upward. We can also define spherical
coordinates, (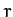 ,
, 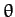 ,
, 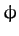 ), whose axis points along the
), whose axis points along the 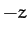 -axis. The latter coordinates are the most convenient, since
-axis. The latter coordinates are the most convenient, since 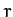 is constrained to always take the value
is constrained to always take the value 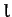 . However, the two angular coordinates,
. However, the two angular coordinates,
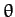 and
and 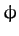 , are free to vary independently. Hence, this is
a two degree of freedom system.
, are free to vary independently. Hence, this is
a two degree of freedom system.
The Cartesian coordinates can be written in terms of the angular coordinates
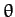 and
and 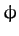 . In fact,
. In fact,
Hence, the potential energy of the system is
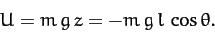 |
(660) |
Also,
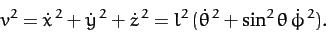 |
(661) |
Thus, the Lagrangian of the system is written
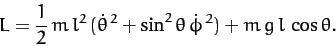 |
(662) |
Note that the Lagrangian is independent of the angular coordinate 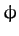 . It
follows that
. It
follows that
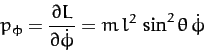 |
(663) |
is a constant of the motion. Of course, 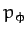 is the angular momentum of
the system about the
is the angular momentum of
the system about the 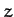 -axis. This is conserved because neither the tension
in the string nor the force of gravity exert a torque about the
-axis. This is conserved because neither the tension
in the string nor the force of gravity exert a torque about the 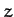 -axis.
Conservation of angular momentum about the
-axis.
Conservation of angular momentum about the 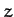 -axis implies that
-axis implies that
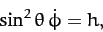 |
(664) |
where 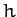 is a constant.
is a constant.
The equation of motion of the system,
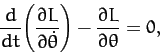 |
(665) |
yields
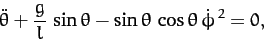 |
(666) |
or
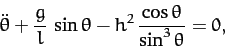 |
(667) |
where use has been made of Equation (664).
Suppose that
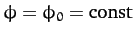 . It follows that
. It follows that
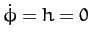 . Hence, Equation (667) yields
. Hence, Equation (667) yields
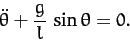 |
(668) |
This, of course, is the equation of a simple pendulum whose motion is
restricted to the vertical plane 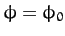 --see Section 3.10.
--see Section 3.10.
Suppose that
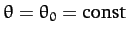 . It follows from Equation (664) that
. It follows from Equation (664) that
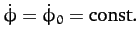 : i.e., the pendulum bob rotates uniformly in a horizontal plane. According
to Equations (664) and (667),
: i.e., the pendulum bob rotates uniformly in a horizontal plane. According
to Equations (664) and (667),
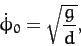 |
(669) |
where
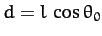 is the vertical distance of the plane of rotation below the pivot point. This type of pendulum is usually called a conical
pendulum, since the string attached to the pendulum bob sweeps out a
cone as the bob rotates.
is the vertical distance of the plane of rotation below the pivot point. This type of pendulum is usually called a conical
pendulum, since the string attached to the pendulum bob sweeps out a
cone as the bob rotates.
Suppose, finally, that the motion is almost conical: i.e., the value
of 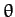 remains close to the value
remains close to the value 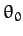 . Let
. Let
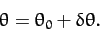 |
(670) |
Taylor expanding Equation (667) to first order in 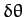 , the zeroth
order terms cancel out, and we are left with
, the zeroth
order terms cancel out, and we are left with
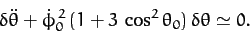 |
(671) |
Hence, solving the above equation, we obtain
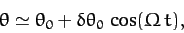 |
(672) |
where
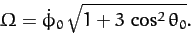 |
(673) |
Thus, the angle 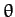 executes simple harmonic motion about its
mean value
executes simple harmonic motion about its
mean value 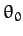 at the angular frequency
at the angular frequency 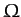 .
.
Now the azimuthal angle, 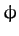 , increases by
, increases by
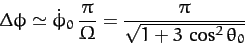 |
(674) |
as the angle of inclination to the vertical, 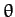 , goes between
successive maxima and minima. Suppose that
, goes between
successive maxima and minima. Suppose that 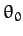 is small.
In this case,
is small.
In this case,
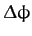 is slightly greater than
is slightly greater than 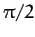 . Now
if
. Now
if
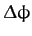 were exactly
were exactly 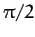 then the pendulum bob would
trace out the outline of a slightly warped circle: i.e., something like the
outline of a potato chip or a saddle. The fact that
then the pendulum bob would
trace out the outline of a slightly warped circle: i.e., something like the
outline of a potato chip or a saddle. The fact that
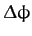 is slightly greater than
is slightly greater than 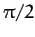 means that this shape precesses about
the
means that this shape precesses about
the 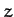 -axis in the same direction as the direction rotation of the bob. The precession rate increases as
the angle of inclination
-axis in the same direction as the direction rotation of the bob. The precession rate increases as
the angle of inclination 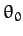 increases. Suppose, now, that
increases. Suppose, now, that 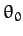 is slightly less than
is slightly less than 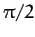 . (Of course,
. (Of course, 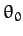 can never exceed
can never exceed 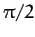 ).
In this case,
).
In this case,
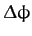 is slightly less than
is slightly less than 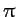 . Now
if
. Now
if
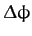 were exactly
were exactly 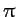 then the pendulum bob would
trace out the outline of a slightly tilted circle. The fact that
then the pendulum bob would
trace out the outline of a slightly tilted circle. The fact that
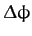 is slightly less than
is slightly less than 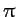 means that this shape
precesses about the
means that this shape
precesses about the 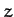 -axis in the opposite direction to the
direction of rotation of the bob. The precession rate increases as the
angle of inclination
-axis in the opposite direction to the
direction of rotation of the bob. The precession rate increases as the
angle of inclination 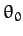 decreases below
decreases below 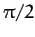 .
.



Next: Exercises
Up: Lagrangian Dynamics
Previous: Generalized Momenta
Richard Fitzpatrick
2011-03-31
![]() and
and ![]() . In fact,
. In fact,
![]() . It
follows that
. It
follows that
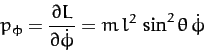
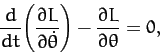
![]() . It follows that
. It follows that
![]() . Hence, Equation (667) yields
. Hence, Equation (667) yields
![]() . It follows from Equation (664) that
. It follows from Equation (664) that
![]() : i.e., the pendulum bob rotates uniformly in a horizontal plane. According
to Equations (664) and (667),
: i.e., the pendulum bob rotates uniformly in a horizontal plane. According
to Equations (664) and (667),
![]() remains close to the value
remains close to the value ![]() . Let
. Let
![]() , increases by
, increases by