


Next: Kepler's Third Law
Up: Planetary Motion
Previous: Kepler's Second Law
Our planet's radial equation of motion, (228), can be combined with
Equation (247) to give
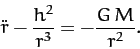 |
(250) |
Suppose that 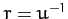 . It follows that
. It follows that
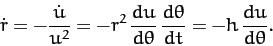 |
(251) |
Likewise,
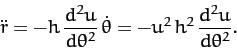 |
(252) |
Hence, Equation (250) can be written in the linear form
 |
(253) |
The general solution to the above equation is
![\begin{displaymath}
u(\theta) = \frac{G\,M}{h^2}\left[1 - e\,\cos(\theta-\theta_0)\right],
\end{displaymath}](img748.png) |
(254) |
where 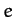 and
and  are arbitrary constants. Without loss of generality, we can
set
are arbitrary constants. Without loss of generality, we can
set 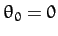 by rotating our coordinate system about the
by rotating our coordinate system about the 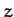 -axis. Thus,
we obtain
-axis. Thus,
we obtain
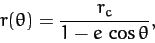 |
(255) |
where
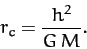 |
(256) |
We immediately recognize Equation (255) as the equation of a conic
section which is confocal with the origin (i.e., with the Sun).
Specifically, for 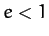 , Equation (255) is the equation of an ellipse
which is confocal with the Sun. Thus, the orbit of our planet
around the Sun in a confocal ellipse--this is Kepler's first law
of planetary motion. Of course, a planet cannot have a parabolic
or a hyperbolic orbit, since such orbits are only appropriate to objects which are ultimately able to escape from the Sun's gravitational field.
, Equation (255) is the equation of an ellipse
which is confocal with the Sun. Thus, the orbit of our planet
around the Sun in a confocal ellipse--this is Kepler's first law
of planetary motion. Of course, a planet cannot have a parabolic
or a hyperbolic orbit, since such orbits are only appropriate to objects which are ultimately able to escape from the Sun's gravitational field.



Next: Kepler's Third Law
Up: Planetary Motion
Previous: Kepler's Second Law
Richard Fitzpatrick
2011-03-31