


Next: Vector Calculus
Up: Vector Algebra and Vector
Previous: Scalar Triple Product
Vector Triple Product
For three vectors 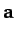 ,
, 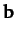 , and
, and 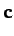 , the vector triple product is defined
, the vector triple product is defined
 . The brackets are important because
. The brackets are important because
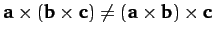 .
In fact, it can be demonstrated that
.
In fact, it can be demonstrated that
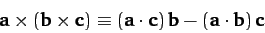 |
(1317) |
and
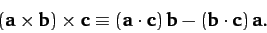 |
(1318) |
Let us try to prove the first of the above theorems. The left-hand side and the
right-hand side are both proper vectors, so if we can prove this result in one particular
coordinate system then it must be true in general. Let us take convenient axes such that
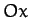 lies along
lies along 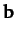 , and
, and 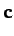 lies in the
lies in the 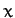 -
-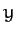 plane. It follows that
plane. It follows that
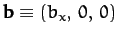 ,
,
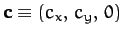 , and
, and
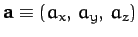 .
The vector
.
The vector
 is directed along
is directed along 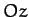 : i.e.,
: i.e.,
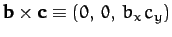 . Hence,
. Hence,
 lies in the
lies in the 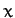 -
-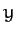 plane: i.e.,
plane: i.e.,
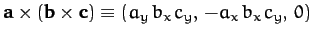 .
This is the left-hand side of Equation (A.1317) in our convenient coordinate system. To evaluate the right-hand side,
we need
.
This is the left-hand side of Equation (A.1317) in our convenient coordinate system. To evaluate the right-hand side,
we need
 and
and
 .
It follows that the right-hand side is
.
It follows that the right-hand side is
which proves the theorem.



Next: Vector Calculus
Up: Vector Algebra and Vector
Previous: Scalar Triple Product
Richard Fitzpatrick
2011-03-31
![]() lies along
lies along ![]() , and
, and ![]() lies in the
lies in the ![]() -
-![]() plane. It follows that
plane. It follows that
![]() ,
,
![]() , and
, and
![]() .
The vector
.
The vector
![]() is directed along
is directed along ![]() : i.e.,
: i.e.,
![]() . Hence,
. Hence,
![]() lies in the
lies in the ![]() -
-![]() plane: i.e.,
plane: i.e.,
![]() .
This is the left-hand side of Equation (A.1317) in our convenient coordinate system. To evaluate the right-hand side,
we need
.
This is the left-hand side of Equation (A.1317) in our convenient coordinate system. To evaluate the right-hand side,
we need
![]() and
and
![]() .
It follows that the right-hand side is
.
It follows that the right-hand side is