


Next: Numerical Solution
Up: The Chaotic Pendulum
Previous: Basic Problem
Analytic Solution
Before attempting a numerical solution of the equations of motion of any dynamical system, it is a good idea to, first, investigate the equations as thoroughly as possible via standard analytic techniques.
Unfortunately, Equations (1237) and (1238) constitute a non-linear dynamical
system--because of the presence of the 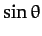 term on the right-hand side of
Equation (1238). This system, like most non-linear systems, does not possess a simple
analytic solution. Fortunately, however, if we restrict our attention to small amplitude oscillations,
such that the approximation
term on the right-hand side of
Equation (1238). This system, like most non-linear systems, does not possess a simple
analytic solution. Fortunately, however, if we restrict our attention to small amplitude oscillations,
such that the approximation
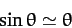 |
(1239) |
is valid,
then the system becomes linear, and can easily be solved analytically.
The linearized equations of motion of the pendulum take the form:
Suppose
that the pendulum's position, 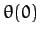 , and velocity,
, and velocity, 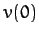 , are specified at time
, are specified at time  .
As is well-known, in this case, the above equations of motion can be solved analytically to give:
.
As is well-known, in this case, the above equations of motion can be solved analytically to give:
Here,
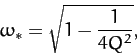 |
(1244) |
and it is assumed that 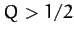 .
It can be seen that the above expressions for
.
It can be seen that the above expressions for  and
and 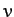 both consist of three
terms. The first two terms clearly represent transients, since they depend on the initial
conditions, and decay exponentially in time--see Section 3.9. In fact, the e-folding time for the decay of these
terms is
both consist of three
terms. The first two terms clearly represent transients, since they depend on the initial
conditions, and decay exponentially in time--see Section 3.9. In fact, the e-folding time for the decay of these
terms is  (in normalized time units).
The final term represents the time-asymptotic motion of the pendulum, and is manifestly independent of the initial conditions--see Section 3.5.
(in normalized time units).
The final term represents the time-asymptotic motion of the pendulum, and is manifestly independent of the initial conditions--see Section 3.5.
Figure 58:
A phase-space plot of the periodic attractor for a linear damped periodically
driven pendulum. Data calculated analytically for  and
and 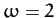 .
.
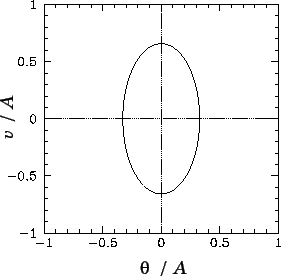 |
It is often convenient to visualize the motion of a dynamical system as an orbit, or trajectory, in
phase-space, which is defined as the space of all of the dynamical variables required to
specify the instantaneous state of the system. For the case in hand, there are two dynamical
variables, 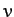 and
and  , and so phase-space corresponds to the
, and so phase-space corresponds to the  -
-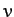 plane. Note that
each different point in this plane corresponds to a unique instantaneous state of the pendulum.
[Strictly speaking, we should also consider
plane. Note that
each different point in this plane corresponds to a unique instantaneous state of the pendulum.
[Strictly speaking, we should also consider 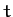 to be a dynamical variable, since it
appears explicitly on the right-hand side of Equation (1238).]
to be a dynamical variable, since it
appears explicitly on the right-hand side of Equation (1238).]
It is clear, from Equations (1242) and (1243), that if we wait long enough for all
of the transients to decay away then the motion of the pendulum settles down to the
following simple orbit in phase-space:
This orbit traces out the closed curve
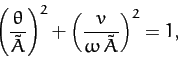 |
(1247) |
in phase-space, where
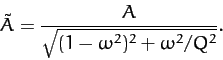 |
(1248) |
As illustrated in Figure 58, this curve is an ellipse whose principal axes are
aligned with the 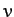 and
and  coordinate axes.
Observe that the curve is closed, which suggests that the associated motion is periodic in time. In fact, the
motion repeats itself exactly every
coordinate axes.
Observe that the curve is closed, which suggests that the associated motion is periodic in time. In fact, the
motion repeats itself exactly every
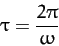 |
(1249) |
normalized time units. The maximum angular displacement of the pendulum from its undriven rest position
(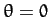 ) is
) is 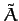 .
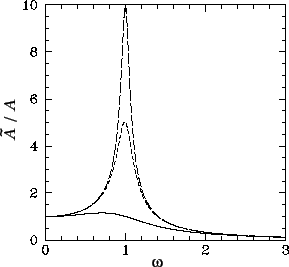
As illustrated in Figure 59, the variation of
.
As illustrated in Figure 59, the variation of 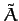 with driving frequency
with driving frequency 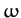 [see Equation (1248)] displays all of the features of a classic resonance curve. The maximum
amplitude of the driven oscillation is proportional to the quality-factor,
[see Equation (1248)] displays all of the features of a classic resonance curve. The maximum
amplitude of the driven oscillation is proportional to the quality-factor,  , and
is achieved when the driving frequency matches the natural
frequency of the pendulum (i.e., when
, and
is achieved when the driving frequency matches the natural
frequency of the pendulum (i.e., when 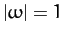 ). Moreover,
the width of the resonance in
). Moreover,
the width of the resonance in 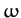 -space
is proportional to
-space
is proportional to 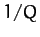 --see Section 3.7.
--see Section 3.7.
Figure 59:
The maximum angular displacement of a linear damped periodically driven
pendulum as a function of driving frequency. The solid curve corresponds to 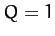 . The
short-dashed curve corresponds to
. The
short-dashed curve corresponds to 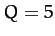 . The long-dashed curve corresponds to
. The long-dashed curve corresponds to 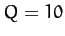 .
Analytic data.
.
Analytic data.
 |
The phase-space curve shown in Figure 58 is called a periodic attractor. It is
termed an ``attractor'' because,
irrespective of the initial conditions, the trajectory of the system in phase-space tends
asymptotically to--in other words, is attracted to--this curve as
 . This
gravitation of phase-space trajectories towards the attractor is illustrated in Figures 60 and
61. Of course, the attractor is termed ``periodic'' because it corresponds to motion which is
periodic in time.
. This
gravitation of phase-space trajectories towards the attractor is illustrated in Figures 60 and
61. Of course, the attractor is termed ``periodic'' because it corresponds to motion which is
periodic in time.
Figure 60:
The phase-space trajectory of a linear damped periodically driven
pendulum. Data calculated analytically for 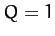 and
and 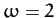 . Here,
. Here, 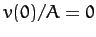 and
and 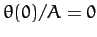 .
.
 |
Figure 61:
The phase-space trajectory of a linear damped periodically driven
pendulum. Data calculated analytically for 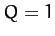 and
and 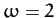 .
Here,
.
Here,  and
and
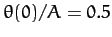 .
.
 |
Let us summarize our findings so far. We have discovered that if a damped pendulum is
subject to a low amplitude periodic drive then its time-asymptotic response (i.e.,
its response after any transients have died away) is periodic, with the same period
as the driving torque. Moreover, the response exhibits resonant behaviour as the driving
frequency approaches the natural frequency of oscillation of the pendulum. The amplitude
of the resonant response, as well as the width of the resonant window, is governed by the
amount of damping in the system. After a little reflection, we can easily appreciate that
all of these results are a direct consequence of the linearity of the pendulum's
equations of motion in the low amplitude limit. In fact,
it is easily demonstrated that the time-asymptotic response of any intrinsically
stable linear system (with a discrete spectrum of normal modes) to a periodic drive is periodic,
with the same period as the drive. Moreover, if the driving frequency approaches
one of the natural frequencies of oscillation of the system then the response exhibits
resonant behaviour. But, is this the only allowable time-asymptotic response of a dynamical system to a
periodic drive? It turns out that it is not.
Indeed, the response of
a non-linear system to a periodic drive is generally much richer and
far more diverse than simple periodic motion. Since the majority of naturally
occurring dynamical systems are non-linear, it is clearly important that we gain a
basic understanding of this phenomenon. Unfortunately, we cannot achieve this goal via
a standard analytic approach, since non-linear equations of motion generally do not possess
simple analytic solutions. Instead, we must employ numerical methods. As an example, let us
investigate the dynamics of a damped pendulum, subject to a periodic drive, with no
restrictions on the amplitude of the pendulum's motion.



Next: Numerical Solution
Up: The Chaotic Pendulum
Previous: Basic Problem
Richard Fitzpatrick
2011-03-31

![]() and
and ![]() , and so phase-space corresponds to the
, and so phase-space corresponds to the ![]() -
-![]() plane. Note that
each different point in this plane corresponds to a unique instantaneous state of the pendulum.
[Strictly speaking, we should also consider
plane. Note that
each different point in this plane corresponds to a unique instantaneous state of the pendulum.
[Strictly speaking, we should also consider ![]() to be a dynamical variable, since it
appears explicitly on the right-hand side of Equation (1238).]
to be a dynamical variable, since it
appears explicitly on the right-hand side of Equation (1238).]
![$\displaystyle \frac{A\left[(1-\omega^2)\,\cos(\omega\, t)+ (\omega/Q)\,\sin(\omega\, t)\right]}
{\left[(1-\omega^2)^2+\omega^2/Q^2\right]},$](img3055.png)
![$\displaystyle \frac{\omega\, A\left[-(1-\omega^2)\,\sin(\omega\, t)+ (\omega/Q)\,\cos(\omega\, t)\right]}
{\left[(1-\omega^2)^2+\omega^2/Q^2\right]}.$](img3056.png)
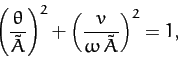

![]() . This
gravitation of phase-space trajectories towards the attractor is illustrated in Figures 60 and
61. Of course, the attractor is termed ``periodic'' because it corresponds to motion which is
periodic in time.
. This
gravitation of phase-space trajectories towards the attractor is illustrated in Figures 60 and
61. Of course, the attractor is termed ``periodic'' because it corresponds to motion which is
periodic in time.

