


Next: Lunar Equations of Motion
Up: Lunar Motion
Previous: Historical Background
Let  and
and 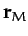 be the position vectors of the Earth and Moon, respectively, in a non-rotating
reference frame in which the Sun is at rest at the origin. Treating this reference frame as inertial (which is an
excellent approximation, given that the mass of the Sun is very much greater than that of the Earth or the Moon--see Chapter 6),
the Earth's
equation of motion becomes (see Chapter 5)
be the position vectors of the Earth and Moon, respectively, in a non-rotating
reference frame in which the Sun is at rest at the origin. Treating this reference frame as inertial (which is an
excellent approximation, given that the mass of the Sun is very much greater than that of the Earth or the Moon--see Chapter 6),
the Earth's
equation of motion becomes (see Chapter 5)
 |
(1119) |
where
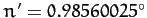 per day and
per day and
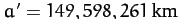 are the mean angular velocity and major radius, respectively, of the
terrestrial orbit about the Sun. Here,
are the mean angular velocity and major radius, respectively, of the
terrestrial orbit about the Sun. Here,
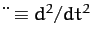 . On the other hand, the Moon's equation of motion takes the form
. On the other hand, the Moon's equation of motion takes the form
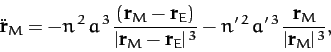 |
(1120) |
where
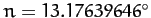 per day and
per day and
 are the mean angular velocity and major radius, respectively, of the lunar
orbit about the Earth. Note that we have retained the perturbing influence (i.e., acceleration) of the Sun in the
lunar equation of motion, (1120), whilst neglecting the perturbing influence of the Moon in the terrestrial
equation of motion, (1119), since the former influence is significantly greater (by a factor
are the mean angular velocity and major radius, respectively, of the lunar
orbit about the Earth. Note that we have retained the perturbing influence (i.e., acceleration) of the Sun in the
lunar equation of motion, (1120), whilst neglecting the perturbing influence of the Moon in the terrestrial
equation of motion, (1119), since the former influence is significantly greater (by a factor
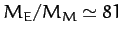 , where
, where 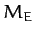 is the mass of the
Earth, and
is the mass of the
Earth, and 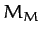 the mass of the Moon) than the latter.
the mass of the Moon) than the latter.
Let
be the position
vectors of the Moon and Sun, respectively, relative to the Earth. It follows, from Equations (1119)-(1122), that in a non-inertial
reference frame, 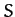 (say), in which the Earth is at rest at the origin, but the coordinate axes point
in fixed directions, the
lunar and solar equations of motion take the form
(say), in which the Earth is at rest at the origin, but the coordinate axes point
in fixed directions, the
lunar and solar equations of motion take the form
respectively.
Let us set up a conventional Cartesian coordinate system in 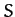 which is such that the (apparent) orbit of the
Sun about the Earth lies in the
which is such that the (apparent) orbit of the
Sun about the Earth lies in the 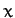 -
-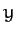 plane. This implies that the
plane. This implies that the
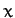 -
-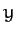 plane corresponds to the so-called ecliptic plane. Accordingly, in
plane corresponds to the so-called ecliptic plane. Accordingly, in 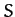 , the Sun
appears to orbit the Earth at the mean angular velocity
, the Sun
appears to orbit the Earth at the mean angular velocity
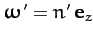 (assuming that the
(assuming that the 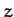 -axis points
toward the so-called north ecliptic pole), whereas the
projection of the Moon onto the ecliptic plane orbits the Earth at the mean angular velocity
-axis points
toward the so-called north ecliptic pole), whereas the
projection of the Moon onto the ecliptic plane orbits the Earth at the mean angular velocity
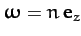 .
.
In the following, for the sake of simplicity, we shall neglect the small eccentricity,
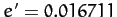 , of the Sun's apparent orbit about the
Earth (which is actually the eccentricity of the Earth's orbit about the Sun), and approximate the solar orbit as a circle, centered on the Earth. Thus, if
, of the Sun's apparent orbit about the
Earth (which is actually the eccentricity of the Earth's orbit about the Sun), and approximate the solar orbit as a circle, centered on the Earth. Thus, if 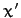 ,
,  ,
, 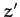 are the Cartesian coordinates of the Sun in
are the Cartesian coordinates of the Sun in 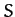 then
an appropriate solution of the solar equation of motion, (1124), is
then
an appropriate solution of the solar equation of motion, (1124), is



Next: Lunar Equations of Motion
Up: Lunar Motion
Previous: Historical Background
Richard Fitzpatrick
2011-03-31
![]() which is such that the (apparent) orbit of the
Sun about the Earth lies in the
which is such that the (apparent) orbit of the
Sun about the Earth lies in the ![]() -
-![]() plane. This implies that the
plane. This implies that the
![]() -
-![]() plane corresponds to the so-called ecliptic plane. Accordingly, in
plane corresponds to the so-called ecliptic plane. Accordingly, in ![]() , the Sun
appears to orbit the Earth at the mean angular velocity
, the Sun
appears to orbit the Earth at the mean angular velocity
![]() (assuming that the
(assuming that the ![]() -axis points
toward the so-called north ecliptic pole), whereas the
projection of the Moon onto the ecliptic plane orbits the Earth at the mean angular velocity
-axis points
toward the so-called north ecliptic pole), whereas the
projection of the Moon onto the ecliptic plane orbits the Earth at the mean angular velocity
![]() .
.
![]() , of the Sun's apparent orbit about the
Earth (which is actually the eccentricity of the Earth's orbit about the Sun), and approximate the solar orbit as a circle, centered on the Earth. Thus, if
, of the Sun's apparent orbit about the
Earth (which is actually the eccentricity of the Earth's orbit about the Sun), and approximate the solar orbit as a circle, centered on the Earth. Thus, if ![]() ,
, ![]() ,
, ![]() are the Cartesian coordinates of the Sun in
are the Cartesian coordinates of the Sun in ![]() then
an appropriate solution of the solar equation of motion, (1124), is
then
an appropriate solution of the solar equation of motion, (1124), is