


Next: Lunar Motion
Up: The Three-Body Problem
Previous: Zero-Velocity Surfaces
We have seen that the five Lagrange points, 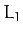 to
to 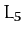 , are the equilibrium points
of mass
, are the equilibrium points
of mass 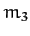 in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
Now, the equations of motion of mass 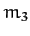 in the co-rotating frame are
specified in Equations (1056)-(1058). Note that the motion
in the
in the co-rotating frame are
specified in Equations (1056)-(1058). Note that the motion
in the  -
-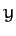 plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the
plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the 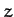 -axis simply
corresponds to motion in the potential
-axis simply
corresponds to motion in the potential 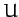 . Hence, the condition for
the stability of the Lagrange points (which all lie at
. Hence, the condition for
the stability of the Lagrange points (which all lie at 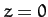 ) to small displacements parallel
to the
) to small displacements parallel
to the 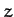 -axis is simply (see Section 3.2)
-axis is simply (see Section 3.2)
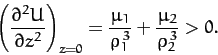 |
(1096) |
This condition is satisfied everywhere in the  -
-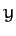 plane. Hence, the Lagrange points are all
stable to small displacements parallel to the
plane. Hence, the Lagrange points are all
stable to small displacements parallel to the 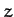 -axis. It, thus, remains to investigate
their stability to small displacements lying within the
-axis. It, thus, remains to investigate
their stability to small displacements lying within the  -
-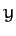 plane.
plane.
Suppose that a Lagrange point is situated in the  -
-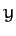 plane at coordinates
plane at coordinates
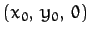 .
Let us consider small amplitude
.
Let us consider small amplitude  -
-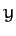 motion in the vicinity of this point by writing
motion in the vicinity of this point by writing
where 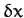 and
and 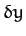 are infinitesimal. Expanding
are infinitesimal. Expanding 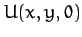 about the Lagrange point as a Taylor series, and retaining terms up to second-order in small
quantities, we obtain
about the Lagrange point as a Taylor series, and retaining terms up to second-order in small
quantities, we obtain
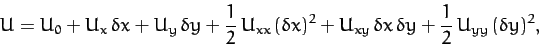 |
(1100) |
where
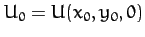 ,
,
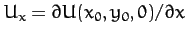 ,
,
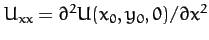 ,
etc. However, by definition,
,
etc. However, by definition, 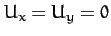 at a Lagrange point, so the expansion simplifies to
at a Lagrange point, so the expansion simplifies to
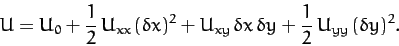 |
(1101) |
Finally, substitution of Equations (1097)-(1099), and (1101)
into the equations of  -
- motion, (1056) and (1057), yields
motion, (1056) and (1057), yields
since  .
.
Let us search for a solution of the above pair of equations
of the form
 and
and
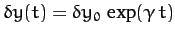 . We obtain
. We obtain
![\begin{displaymath}
\left(
\begin{array}{cc}
\gamma^2 + U_{xx}& -2\,\gamma+U_{xy...
... = \left(
\begin{array}{c}
0\\ [0.5ex]
0
\end{array}\right).
\end{displaymath}](img2651.png) |
(1104) |
This equation only has a non-trivial solution if the determinant of the
matrix is zero. Hence, we get
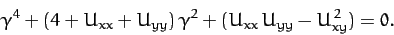 |
(1105) |
Now, it is convenient to define
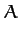 |
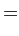 |
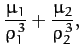 |
(1106) |
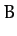 |
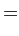 |
![$\displaystyle 3\left[ \frac{\mu_1}{\rho_1^{\,5}} + \frac{\mu_2}{\rho_2^{\,5}}\right]y^2,$](img2656.png) |
(1107) |
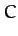 |
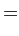 |
![$\displaystyle 3\left[\frac{\mu_1\,(x+\mu_2)}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)}{\rho_2^{\,5}}\right]y,$](img2658.png) |
(1108) |
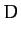 |
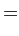 |
![$\displaystyle 3\left[\frac{\mu_1\,(x+\mu_2)^2}{\rho_1^{\,3}}+\frac{\mu_2\,(x-\mu_1)^2}{\rho_2^{\,3}}\right],$](img2660.png) |
(1109) |
where all terms are evaluated at the point
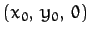 . It thus follows that
. It thus follows that
Consider the co-linear Lagrange points, 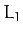 ,
, 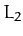 , and
, and 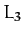 . These all
lie on the
. These all
lie on the  -axis, and are thus characterized by
-axis, and are thus characterized by
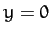 ,
,
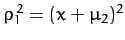 , and
, and
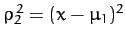 . It follows,
from the above equations, that
. It follows,
from the above equations, that 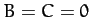 and
and 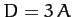 . Hence,
. Hence,
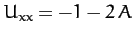 ,
,
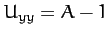 , and
, and 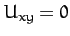 . Equation (1105) thus yields
. Equation (1105) thus yields
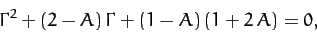 |
(1113) |
where
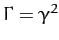 . Now, in order for a Lagrange point to be stable
to small displacements, all four of the roots,
. Now, in order for a Lagrange point to be stable
to small displacements, all four of the roots, 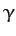 , of Equation (1105) must
be purely imaginary. This, in turn, implies that the two roots of
the above equation,
, of Equation (1105) must
be purely imaginary. This, in turn, implies that the two roots of
the above equation,
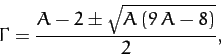 |
(1114) |
must both be real and negative.
Thus, the stability criterion is
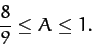 |
(1115) |
Figure 56 shows 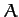 calculated at the three co-linear Lagrange points as a function of
calculated at the three co-linear Lagrange points as a function of 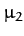 , for all
allowed values of this parameter (i.e.,
, for all
allowed values of this parameter (i.e.,
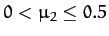 ). It can be seen that
). It can be seen that 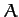 is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points,
is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points, 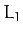 ,
, 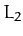 , and
, and 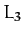 , are intrinsically unstable equilibrium points in the co-rotating
frame.
, are intrinsically unstable equilibrium points in the co-rotating
frame.
Figure 56:
The solid, short-dashed, and long-dashed curves show 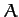 as a function of
as a function of 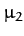 at the
at the
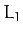 ,
, 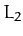 , and
, and 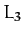 Lagrange points.
Lagrange points.
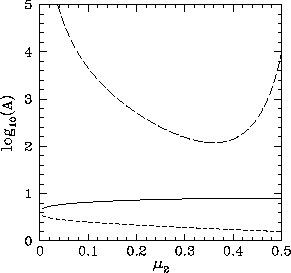 |
Let us now consider the triangular Lagrange points, 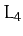 and
and 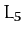 . These points
are characterized by
. These points
are characterized by
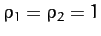 . It follows that
. It follows that 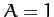 ,
, 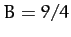 ,
,
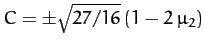 ,
and
,
and 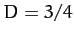 . Hence,
. Hence, 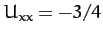 ,
, 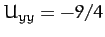 , and
, and
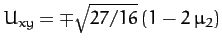 ,
where the upper/lower signs corresponds to
,
where the upper/lower signs corresponds to  and
and 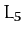 , respectively.
Equation (1105) thus yields
, respectively.
Equation (1105) thus yields
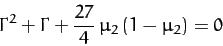 |
(1116) |
for both points,
where
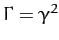 . As before, the stability criterion is that the two roots of the
above equation must both be
real and negative. This is the case provided that
. As before, the stability criterion is that the two roots of the
above equation must both be
real and negative. This is the case provided that
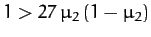 , which
yields the stability criterion
, which
yields the stability criterion
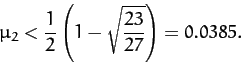 |
(1117) |
In unnormalized units, this criterion becomes
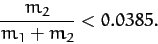 |
(1118) |
We thus conclude that the 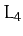 and
and 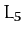 Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass
Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass 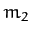 is less than about
is less than about 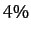 of
mass
of
mass 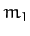 . If this is the case then mass
. If this is the case then mass 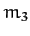 can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass
can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass 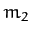 about mass
about mass 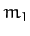 , but will stay approximately
, but will stay approximately 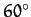 ahead of
mass
ahead of
mass 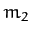 , if it is orbiting the
, if it is orbiting the 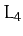 point, or
point, or 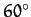 behind, if it is orbiting the
behind, if it is orbiting the 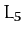 point--see Figure 55. This type of behavior has been observed in the Solar System. For instance,
there is a sub-class of asteroids, known as the Trojan asteroids, which are trapped
in the vicinity of the
point--see Figure 55. This type of behavior has been observed in the Solar System. For instance,
there is a sub-class of asteroids, known as the Trojan asteroids, which are trapped
in the vicinity of the 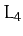 and
and 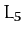 points of the Sun-Jupiter system (which easily
satisfies the above stability criterion), and consequently share Jupiter's orbit around the Sun,
staying approximately
points of the Sun-Jupiter system (which easily
satisfies the above stability criterion), and consequently share Jupiter's orbit around the Sun,
staying approximately 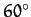 ahead of, and
ahead of, and 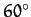 behind, Jupiter, respectively.
Furthermore, the
behind, Jupiter, respectively.
Furthermore, the 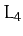 and
and 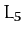 points of the Sun-Earth system are occupied by clouds of dust.
points of the Sun-Earth system are occupied by clouds of dust.



Next: Lunar Motion
Up: The Three-Body Problem
Previous: Zero-Velocity Surfaces
Richard Fitzpatrick
2011-03-31
![]() in the co-rotating frame are
specified in Equations (1056)-(1058). Note that the motion
in the
in the co-rotating frame are
specified in Equations (1056)-(1058). Note that the motion
in the ![]() -
-![]() plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the
plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the ![]() -axis simply
corresponds to motion in the potential
-axis simply
corresponds to motion in the potential ![]() . Hence, the condition for
the stability of the Lagrange points (which all lie at
. Hence, the condition for
the stability of the Lagrange points (which all lie at ![]() ) to small displacements parallel
to the
) to small displacements parallel
to the ![]() -axis is simply (see Section 3.2)
-axis is simply (see Section 3.2)
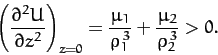
![]() -
-![]() plane at coordinates
plane at coordinates
![]() .
Let us consider small amplitude
.
Let us consider small amplitude ![]() -
-![]() motion in the vicinity of this point by writing
motion in the vicinity of this point by writing
![]() and
and
![]() . We obtain
. We obtain
![\begin{displaymath}
\left(
\begin{array}{cc}
\gamma^2 + U_{xx}& -2\,\gamma+U_{xy...
... = \left(
\begin{array}{c}
0\\ [0.5ex]
0
\end{array}\right).
\end{displaymath}](img2651.png)
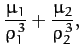
![$\displaystyle 3\left[ \frac{\mu_1}{\rho_1^{\,5}} + \frac{\mu_2}{\rho_2^{\,5}}\right]y^2,$](img2656.png)
![$\displaystyle 3\left[\frac{\mu_1\,(x+\mu_2)}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)}{\rho_2^{\,5}}\right]y,$](img2658.png)
![$\displaystyle 3\left[\frac{\mu_1\,(x+\mu_2)^2}{\rho_1^{\,3}}+\frac{\mu_2\,(x-\mu_1)^2}{\rho_2^{\,3}}\right],$](img2660.png)
![]() ,
, ![]() , and
, and ![]() . These all
lie on the
. These all
lie on the ![]() -axis, and are thus characterized by
-axis, and are thus characterized by
![]() ,
,
![]() , and
, and
![]() . It follows,
from the above equations, that
. It follows,
from the above equations, that ![]() and
and ![]() . Hence,
. Hence,
![]() ,
,
![]() , and
, and ![]() . Equation (1105) thus yields
. Equation (1105) thus yields
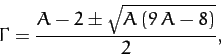

![]() and
and ![]() . These points
are characterized by
. These points
are characterized by
![]() . It follows that
. It follows that ![]() ,
, ![]() ,
,
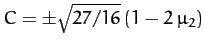 ,
and
,
and ![]() . Hence,
. Hence, ![]() ,
, ![]() , and
, and
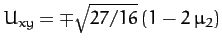 ,
where the upper/lower signs corresponds to
,
where the upper/lower signs corresponds to ![]() and
and ![]() , respectively.
Equation (1105) thus yields
, respectively.
Equation (1105) thus yields
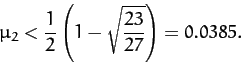
![]() and
and ![]() Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass
Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass ![]() is less than about
is less than about ![]() of
mass
of
mass ![]() . If this is the case then mass
. If this is the case then mass ![]() can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass
can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass ![]() about mass
about mass ![]() , but will stay approximately
, but will stay approximately ![]() ahead of
mass
ahead of
mass ![]() , if it is orbiting the
, if it is orbiting the ![]() point, or
point, or ![]() behind, if it is orbiting the
behind, if it is orbiting the ![]() point--see Figure 55. This type of behavior has been observed in the Solar System. For instance,
there is a sub-class of asteroids, known as the Trojan asteroids, which are trapped
in the vicinity of the
point--see Figure 55. This type of behavior has been observed in the Solar System. For instance,
there is a sub-class of asteroids, known as the Trojan asteroids, which are trapped
in the vicinity of the ![]() and
and ![]() points of the Sun-Jupiter system (which easily
satisfies the above stability criterion), and consequently share Jupiter's orbit around the Sun,
staying approximately
points of the Sun-Jupiter system (which easily
satisfies the above stability criterion), and consequently share Jupiter's orbit around the Sun,
staying approximately ![]() ahead of, and
ahead of, and ![]() behind, Jupiter, respectively.
Furthermore, the
behind, Jupiter, respectively.
Furthermore, the ![]() and
and ![]() points of the Sun-Earth system are occupied by clouds of dust.
points of the Sun-Earth system are occupied by clouds of dust.