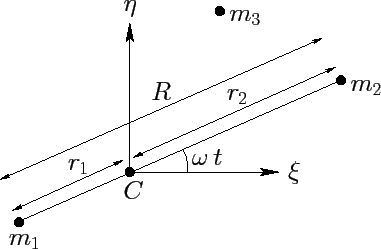
 |
Let us define a Cartesian coordinate system
![]() in an inertial reference frame whose
origin coincides with the center of mass,
in an inertial reference frame whose
origin coincides with the center of mass, ![]() , of the two orbiting masses. Furthermore, let the orbital plane of these masses
coincide with the
, of the two orbiting masses. Furthermore, let the orbital plane of these masses
coincide with the ![]() -
-![]() plane, and let them both lie on the
plane, and let them both lie on the ![]() -axis at time
-axis at time ![]() --see Figure 47.
Suppose that
--see Figure 47.
Suppose that ![]() is the constant distance between the two orbiting masses,
is the constant distance between the two orbiting masses, ![]() the constant distance
between mass
the constant distance
between mass ![]() and the origin, and
and the origin, and ![]() the constant distance between mass
the constant distance between mass ![]() and the origin. Moreover,
let
and the origin. Moreover,
let ![]() be the constant orbital angular velocity. It follows, from Section 6.3,
that
be the constant orbital angular velocity. It follows, from Section 6.3,
that
It is convenient to choose our unit of length such that ![]() , and our unit of
mass such that
, and our unit of
mass such that ![]() . It follows, from Equation (1030), that
. It follows, from Equation (1030), that ![]() . However, we shall continue to
retain
. However, we shall continue to
retain ![]() in our equations, for the sake of clarity. Let
in our equations, for the sake of clarity. Let ![]() , and
, and
![]() . It is easily demonstrated
that
. It is easily demonstrated
that ![]() , and
, and
![]() . Hence, the two orbiting masses,
. Hence, the two orbiting masses, ![]() and
and ![]() , have position
vectors
, have position
vectors
![]() and
and
![]() , respectively, where (see Figure 47)
, respectively, where (see Figure 47)