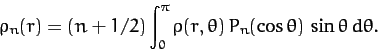Next: Potential Due to a
Up: Gravitational Potential Theory
Previous: Gravitational Potential
Axially Symmetric Mass Distributions
At this point, it is convenient to adopt standard spherical coordinates,
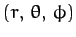 , aligned along the
, aligned along the 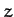 -axis. These coordinates are related to
regular Cartesian coordinates as follows (see Section A.17):
-axis. These coordinates are related to
regular Cartesian coordinates as follows (see Section A.17):
Consider an axially symmetric mass distribution: i.e., a 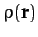 which is independent of the azimuthal angle,
which is independent of the azimuthal angle, 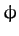 . We would expect
such a mass distribution to generated an axially symmetric gravitational
potential,
. We would expect
such a mass distribution to generated an axially symmetric gravitational
potential,
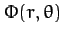 . Hence, without loss of generality, we can
set
. Hence, without loss of generality, we can
set 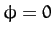 when evaluating
when evaluating 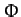 from Equation (868). In fact,
given that
from Equation (868). In fact,
given that
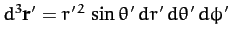 in spherical coordinates, this equation yields
in spherical coordinates, this equation yields
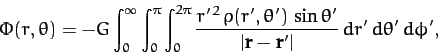 |
(872) |
with the right-hand side evaluated at 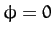 . However, since
. However, since
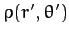 is independent of
is independent of 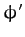 , the above equation
can also be written
, the above equation
can also be written
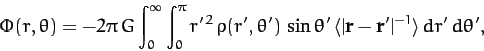 |
(873) |
where
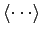 denotes an average over the azimuthal angle,
denotes an average over the azimuthal angle,
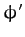 .
.
Now,
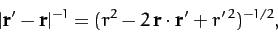 |
(874) |
and
 |
(875) |
where (at 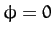 )
)
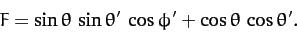 |
(876) |
Hence,
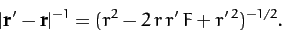 |
(877) |
Suppose that 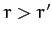 . In this case, we can expand
. In this case, we can expand
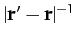 as a convergent power series in
as a convergent power series in 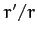 , to give
, to give
![\begin{displaymath}
\vert{\bf r}'-{\bf r}\vert^{-1}= \frac{1}{r}\left[
1 + \left...
...ght)^2(3\,F^2-1)
+ {\cal O}\left(\frac{r'}{r}\right)^3\right].
\end{displaymath}](img2090.png) |
(878) |
Let us now average this expression over the azimuthal angle, 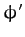 . Since
. Since
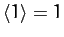 ,
,
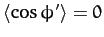 , and
, and
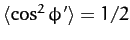 , it is easily seen that
, it is easily seen that
Hence,
Now, the well-known Legendre polynomials, 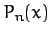 , are defined
, are defined
![\begin{displaymath}
P_n(x) = \frac{1}{2^n\,n!}\,\frac{d^n}{dx^n}\!\left[(x^2-1)^n\right],
\end{displaymath}](img2103.png) |
(882) |
for 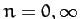 .
It follows that
.
It follows that
etc.
The Legendre polynomials are mutually
orthogonal: i.e.,
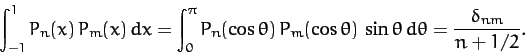 |
(886) |
Here, 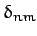 is 1 if
is 1 if 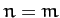 , and 0 otherwise. The Legendre polynomials also form a complete set: i.e., any well-behaved function
of
, and 0 otherwise. The Legendre polynomials also form a complete set: i.e., any well-behaved function
of  can be represented as a weighted sum of the
can be represented as a weighted sum of the 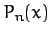 . Likewise,
any well-behaved (even) function of
. Likewise,
any well-behaved (even) function of 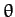 can be represented as a weighted
sum of the
can be represented as a weighted
sum of the
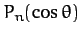 .
.
A comparison of Equation (881) and Equations (883)-(885) makes it reasonably clear that, when 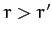 , the complete expansion
of
, the complete expansion
of
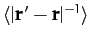 is
is
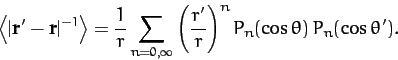 |
(887) |
Similarly, when 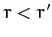 , we can expand in powers of
, we can expand in powers of 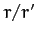 to obtain
to obtain
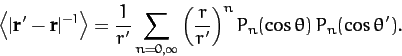 |
(888) |
It follows from Equations (873), (887), and (888)
that
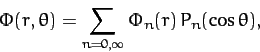 |
(889) |
where
Now, given that the
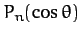 form a complete set, we can always
write
form a complete set, we can always
write
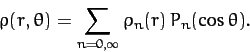 |
(891) |
This expression can be inverted, with the aid of Equation (886), to
give
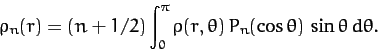 |
(892) |
Hence, Equation (890) reduces to
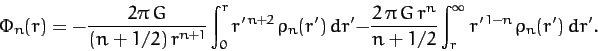 |
(893) |
Thus, we now have a general expression for the gravitational potential,
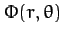 ,
generated by any axially symmetric mass distribution,
,
generated by any axially symmetric mass distribution,
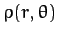 .
.



Next: Potential Due to a
Up: Gravitational Potential Theory
Previous: Gravitational Potential
Richard Fitzpatrick
2011-03-31
![]() which is independent of the azimuthal angle,
which is independent of the azimuthal angle, ![]() . We would expect
such a mass distribution to generated an axially symmetric gravitational
potential,
. We would expect
such a mass distribution to generated an axially symmetric gravitational
potential,
![]() . Hence, without loss of generality, we can
set
. Hence, without loss of generality, we can
set ![]() when evaluating
when evaluating ![]() from Equation (868). In fact,
given that
from Equation (868). In fact,
given that
![]() in spherical coordinates, this equation yields
in spherical coordinates, this equation yields
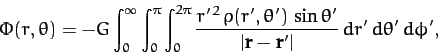
![]() . In this case, we can expand
. In this case, we can expand
![]() as a convergent power series in
as a convergent power series in ![]() , to give
, to give
![\begin{displaymath}
\vert{\bf r}'-{\bf r}\vert^{-1}= \frac{1}{r}\left[
1 + \left...
...ght)^2(3\,F^2-1)
+ {\cal O}\left(\frac{r'}{r}\right)^3\right].
\end{displaymath}](img2090.png)
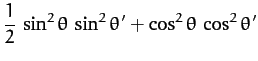
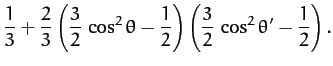
![]() , are defined
, are defined
![]() , the complete expansion
of
, the complete expansion
of
![]() is
is
![]() form a complete set, we can always
write
form a complete set, we can always
write