


Next: Stability Equations
Up: Coupled Oscillations
Previous: Introduction
Consider an 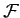 degree of freedom dynamical system described by the
generalized coordinates
degree of freedom dynamical system described by the
generalized coordinates 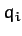 , for
, for 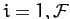 . Suppose that the
kinetic energy
. Suppose that the
kinetic energy 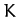 and the potential energy
and the potential energy  are not explicit
functions of time. This implies that the system in question
is isolated: i.e., it is not subject to any external forces or
time-varying constraints. In virtually all dynamical systems of interest, the kinetic
energy can be expressed as a quadratic form: i.e.,
are not explicit
functions of time. This implies that the system in question
is isolated: i.e., it is not subject to any external forces or
time-varying constraints. In virtually all dynamical systems of interest, the kinetic
energy can be expressed as a quadratic form: i.e.,
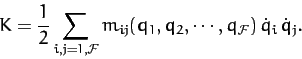 |
(770) |
Without loss of generality, we can specify that the weights 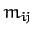 in the above form are
invariant under interchange of the indices
in the above form are
invariant under interchange of the indices 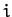 and
and  : i.e.,
: i.e.,
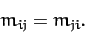 |
(771) |
Finally, the potential energy is written
 .
.
Suppose that 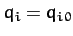 , for
, for 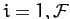 , corresponds to an
equilibrium state of the system. It follows that
, corresponds to an
equilibrium state of the system. It follows that
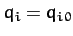 and
and
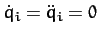 , for
, for 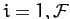 , should be a possible solution of the equations of motion.
Now, Lagrange's equations of motion for the system take the form [see
Equation (613)]
, should be a possible solution of the equations of motion.
Now, Lagrange's equations of motion for the system take the form [see
Equation (613)]
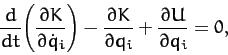 |
(772) |
for 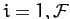 . Here, we have made use of the definition
. Here, we have made use of the definition  , and
the fact that
, and
the fact that  is independent of the
is independent of the 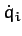 . Now, it is clear, from
an examination of Equation (770), that every component making up
the first two terms in the above equation contains either a
. Now, it is clear, from
an examination of Equation (770), that every component making up
the first two terms in the above equation contains either a 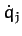 or
a
or
a 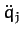 , for some
, for some  . But, we can set all of the generalized velocities
and accelerations to zero in an equilibrium state of the system.
Hence, the first two terms in the above equation are zero, and the
condition for equilibrium reduces to
. But, we can set all of the generalized velocities
and accelerations to zero in an equilibrium state of the system.
Hence, the first two terms in the above equation are zero, and the
condition for equilibrium reduces to
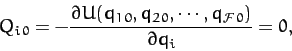 |
(773) |
for 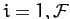 . In other words,
. In other words, 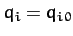 , for
, for 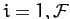 , is an equilibrium
state provided that all of the generalized forces,
, is an equilibrium
state provided that all of the generalized forces, 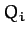 [see Equation (599)], evaluated at
[see Equation (599)], evaluated at 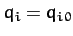 ,
are zero. Let us suppose that this is the case.
,
are zero. Let us suppose that this is the case.



Next: Stability Equations
Up: Coupled Oscillations
Previous: Introduction
Richard Fitzpatrick
2011-03-31
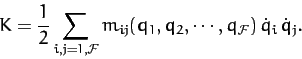
![]() , for
, for ![]() , corresponds to an
equilibrium state of the system. It follows that
, corresponds to an
equilibrium state of the system. It follows that
![]() and
and
![]() , for
, for ![]() , should be a possible solution of the equations of motion.
Now, Lagrange's equations of motion for the system take the form [see
Equation (613)]
, should be a possible solution of the equations of motion.
Now, Lagrange's equations of motion for the system take the form [see
Equation (613)]