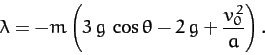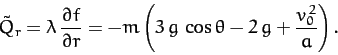Next: Hamilton's Equations
Up: Hamiltonian Dynamics
Previous: Hamilton's Principle
Suppose that we have a dynamical system described by two generalized
coordinates,  and
and 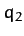 . Suppose, further, that
. Suppose, further, that  and
and 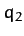 are
not independent variables. In other words,
are
not independent variables. In other words,  and
and 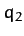 are connected
via some constraint equation of the form
are connected
via some constraint equation of the form
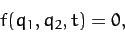 |
(714) |
where 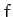 is some function of three variables.
This type of constraint is called a holonomic. [A general
holonomic constraint is of the form
is some function of three variables.
This type of constraint is called a holonomic. [A general
holonomic constraint is of the form
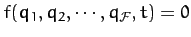 .]
Let
.]
Let
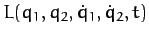 be the Lagrangian.
How do we write the Lagrangian equations of motion of the system?
be the Lagrangian.
How do we write the Lagrangian equations of motion of the system?
Well, according to Hamilton's principle,
![\begin{displaymath}
\delta\int_{t_1}^{t_2} L\,dt = \int_{t_1}^{t_2}\left\{\left[...
... L}{\partial \dot{q}_2}\right)\right]\delta q_2 \right\} dt=0.
\end{displaymath}](img1798.png) |
(715) |
However, at any given instant in time, 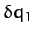 and
and 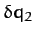 are not independent. Indeed,
Equation (714) yields
are not independent. Indeed,
Equation (714) yields
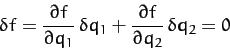 |
(716) |
at a fixed time. Eliminating 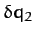 from Equation (715), we obtain
from Equation (715), we obtain
![\begin{displaymath}
\int_{t_1}^{t_2}\left\{\left[
\frac{\partial L}{\partial q_1...
...ht]\frac{1}{\partial f/\partial q_2}\right\} \delta q_1\,dt=0.
\end{displaymath}](img1802.png) |
(717) |
This equation must be satisfied for all possible perturbations  , which implies that the term enclosed in curly brackets is zero.
Hence, we obtain
, which implies that the term enclosed in curly brackets is zero.
Hence, we obtain
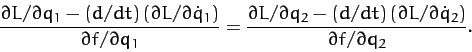 |
(718) |
One obvious way in which we can solve this equation is to separately set both sides
equal to the same function of time, which
we shall denote 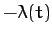 . It follows that the Lagrangian equations of
motion of the system can be written
. It follows that the Lagrangian equations of
motion of the system can be written
In principle, the above two equations can be solved, together with the constraint equation (714), to give 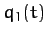 ,
,  , and the
so-called Lagrange multiplier
, and the
so-called Lagrange multiplier 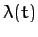 .
Equation (719) can be rewritten
.
Equation (719) can be rewritten
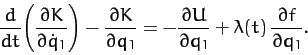 |
(721) |
Now, the generalized force conjugate to
the generalized coordinate  is [see Equation (599)]
is [see Equation (599)]
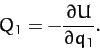 |
(722) |
By analogy, it seems clear from Equation (721) that the generalized constraint force [i.e., the generalized force responsible for maintaining the constraint
(714)] conjugate to  takes the form
takes the form
 |
(723) |
with a similar expression for the generalized constraint force conjugate to 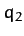 .
.
Suppose, now, that we have a dynamical system described by 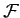 generalized coordinates
generalized coordinates 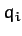 , for
, for 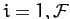 , which is subject to the
holonomic constraint
, which is subject to the
holonomic constraint
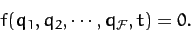 |
(724) |
A simple extension of above analysis yields following the Lagrangian equations of motion of the
system,
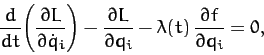 |
(725) |
for 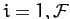 . As before,
. As before,
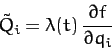 |
(726) |
is the generalized constraint force conjugate to 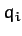 .
Finally, the generalization to multiple holonomic constraints is straightforward.
.
Finally, the generalization to multiple holonomic constraints is straightforward.
Figure 36:
A cylinder rolling down an inclined plane.
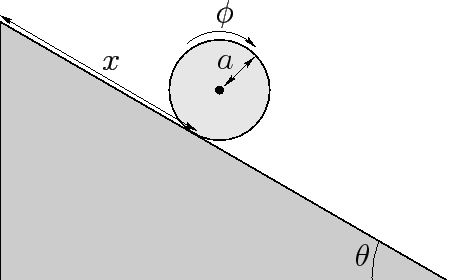 |
Consider the following example. A cylinder of radius  rolls without slipping down a plane
inclined at an angle
rolls without slipping down a plane
inclined at an angle 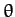 to the horizontal. Let
to the horizontal. Let 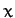 represent the downward displacement of the center of mass of the cylinder parallel to the surface of the plane, and let
represent the downward displacement of the center of mass of the cylinder parallel to the surface of the plane, and let 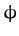 represent the angle of rotation of the cylinder about
its symmetry axis. The fact that the cylinder is rolling without slipping
implies that
represent the angle of rotation of the cylinder about
its symmetry axis. The fact that the cylinder is rolling without slipping
implies that 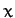 and
and 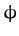 are interrelated via the well-known constraint
are interrelated via the well-known constraint
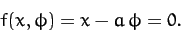 |
(727) |
The Lagrangian of the cylinder takes the form
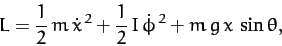 |
(728) |
where  is the cylinder's mass,
is the cylinder's mass, 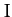 its moment of inertia, and
its moment of inertia, and 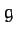 the acceleration due to gravity.
the acceleration due to gravity.
Note that
 and
and
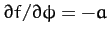 . Hence,
Equation (725) yields the following Lagrangian equations of motion:
. Hence,
Equation (725) yields the following Lagrangian equations of motion:
Equations (727), (729), and (730) can be solved to
give
The generalized constraint force conjugate to 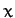 is
is
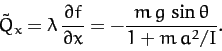 |
(734) |
This represents the frictional force acting parallel to the plane which
impedes the downward acceleration of the cylinder, causing it to be less than the standard value
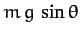 . The
generalized constraint force conjugate to
. The
generalized constraint force conjugate to 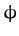 is
is
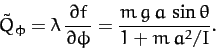 |
(735) |
This represents the frictional torque acting on the cylinder which forces the
cylinder to rotate in such a manner that the constraint (727) is
always satisfied.
Consider a second example. A bead of mass  slides without friction
on a vertical circular hoop of radius
slides without friction
on a vertical circular hoop of radius  . Let
. Let 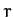 be the
radial coordinate of the bead, and let
be the
radial coordinate of the bead, and let 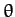 be its
angular coordinate, with the lowest point on the hoop corresponding
to
be its
angular coordinate, with the lowest point on the hoop corresponding
to 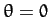 . Both coordinates are measured relative to the
center of the hoop. Now, the bead is constrained to slide along the wire, which implies that
. Both coordinates are measured relative to the
center of the hoop. Now, the bead is constrained to slide along the wire, which implies that
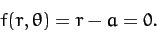 |
(736) |
Note that
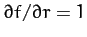 and
and
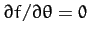 .
The Lagrangian of the system takes the form
.
The Lagrangian of the system takes the form
 |
(737) |
Hence, according to Equation (725), the Lagrangian equations of motion
of the system are written
The second of these equations can be integrated (by multiplying by 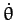 ), subject to the constraint (736), to give
), subject to the constraint (736), to give
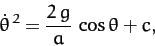 |
(740) |
where 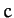 is a constant. Let
is a constant. Let 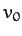 be the tangential velocity of the
bead at the bottom of the hoop (i.e., at
be the tangential velocity of the
bead at the bottom of the hoop (i.e., at 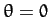 ). It follows that
). It follows that
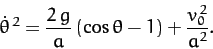 |
(741) |
Equations (736), (738), and (741) can be combined to give
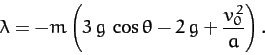 |
(742) |
Finally, the constraint force conjugate to 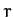 is given by
is given by
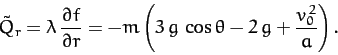 |
(743) |
This represents the radial reaction exerted on the bead by the hoop. Of course,
there is no constraint force conjugate to 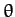 (since
(since
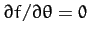 ) because the bead slides without friction.
) because the bead slides without friction.



Next: Hamilton's Equations
Up: Hamiltonian Dynamics
Previous: Hamilton's Principle
Richard Fitzpatrick
2011-03-31
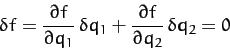
![\begin{displaymath}
\int_{t_1}^{t_2}\left\{\left[
\frac{\partial L}{\partial q_1...
...ht]\frac{1}{\partial f/\partial q_2}\right\} \delta q_1\,dt=0.
\end{displaymath}](img1802.png)
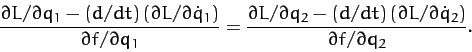
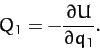

![]() generalized coordinates
generalized coordinates ![]() , for
, for ![]() , which is subject to the
holonomic constraint
, which is subject to the
holonomic constraint
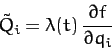
![]() rolls without slipping down a plane
inclined at an angle
rolls without slipping down a plane
inclined at an angle ![]() to the horizontal. Let
to the horizontal. Let ![]() represent the downward displacement of the center of mass of the cylinder parallel to the surface of the plane, and let
represent the downward displacement of the center of mass of the cylinder parallel to the surface of the plane, and let ![]() represent the angle of rotation of the cylinder about
its symmetry axis. The fact that the cylinder is rolling without slipping
implies that
represent the angle of rotation of the cylinder about
its symmetry axis. The fact that the cylinder is rolling without slipping
implies that ![]() and
and ![]() are interrelated via the well-known constraint
are interrelated via the well-known constraint
![]() and
and
![]() . Hence,
Equation (725) yields the following Lagrangian equations of motion:
. Hence,
Equation (725) yields the following Lagrangian equations of motion:
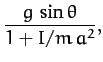
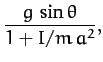
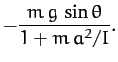
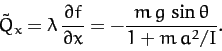
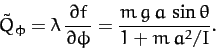
![]() slides without friction
on a vertical circular hoop of radius
slides without friction
on a vertical circular hoop of radius ![]() . Let
. Let ![]() be the
radial coordinate of the bead, and let
be the
radial coordinate of the bead, and let ![]() be its
angular coordinate, with the lowest point on the hoop corresponding
to
be its
angular coordinate, with the lowest point on the hoop corresponding
to ![]() . Both coordinates are measured relative to the
center of the hoop. Now, the bead is constrained to slide along the wire, which implies that
. Both coordinates are measured relative to the
center of the hoop. Now, the bead is constrained to slide along the wire, which implies that