


Next: Lagrangian Dynamics
Up: Rigid Body Rotation
Previous: Rotational Stability
- Find the principal axes of rotation and the principal moments of inertia for a
thin uniform rectangular plate of mass
 and dimensions
and dimensions 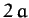 by
by  for rotation
about axes passing through (a) the center of mass, and (b) a corner.
for rotation
about axes passing through (a) the center of mass, and (b) a corner.
- A rigid body having an axis of symmetry rotates freely about a fixed point under no
torques. If
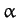 is the angle between the symmetry axis and the instantaneous axis of
rotation, show that the angle between the axis of rotation and the invariable line
(the
is the angle between the symmetry axis and the instantaneous axis of
rotation, show that the angle between the axis of rotation and the invariable line
(the 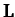 vector) is
vector) is
where  (the moment of inertia about the symmetry axis) is greater than
(the moment of inertia about the symmetry axis) is greater than 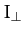 (the moment of inertia about an axis normal to the symmetry axis).
(the moment of inertia about an axis normal to the symmetry axis).
- Since the greatest value of
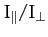 is 2 (symmetrical lamina) show
from the previous result that the angle between the angular velocity and angular momentum
vectors cannot exceed
is 2 (symmetrical lamina) show
from the previous result that the angle between the angular velocity and angular momentum
vectors cannot exceed
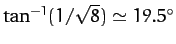 . Find the corresponding
value of
. Find the corresponding
value of 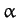 .
.
- A thin uniform rod of length
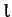 and mass
and mass  is constrained to rotate
with constant angular velocity
is constrained to rotate
with constant angular velocity  about an axis passing through the
center of the rod, and making an angle
about an axis passing through the
center of the rod, and making an angle 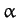 with the rod.
Show that the angular momentum about the center of the rod is perpendicular to the rod, and is of magnitude
with the rod.
Show that the angular momentum about the center of the rod is perpendicular to the rod, and is of magnitude
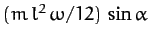 . Show that
the torque is perpendicular to both the rod and the angular momentum vector,
and is of magnitude
. Show that
the torque is perpendicular to both the rod and the angular momentum vector,
and is of magnitude
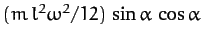 .
.
- A thin uniform disk of radius
 and mass
and mass  is constrained to rotate
with constant angular velocity
is constrained to rotate
with constant angular velocity  about an axis passing through its center, and making an angle
about an axis passing through its center, and making an angle 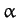 with the normal to the disk.
Find the angular momentum about the center of the disk, as
well as the torque acting on the disk.
with the normal to the disk.
Find the angular momentum about the center of the disk, as
well as the torque acting on the disk.
- Demonstrate that for an isolated rigid body which possesses an
axis of symmetry, and rotates about one of its principal axes, the motion is
only stable to small perturbations if the principal axis is that which corresponds to the
symmetry axis.



Next: Lagrangian Dynamics
Up: Rigid Body Rotation
Previous: Rotational Stability
Richard Fitzpatrick
2011-03-31
![\begin{displaymath}
\tan^{-1}\left[\frac{(I_\parallel-I_\perp)\,\tan\alpha}{I_\parallel+I_\perp\,\tan^2\alpha}\right]
\end{displaymath}](img1554.png)
![\begin{displaymath}
\tan^{-1}\left[\frac{(I_\parallel-I_\perp)\,\tan\alpha}{I_\parallel+I_\perp\,\tan^2\alpha}\right]
\end{displaymath}](img1554.png)