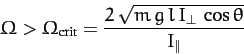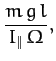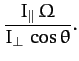Next: Rotational Stability
Up: Rigid Body Rotation
Previous: Eulerian Angles
Gyroscopic Precession
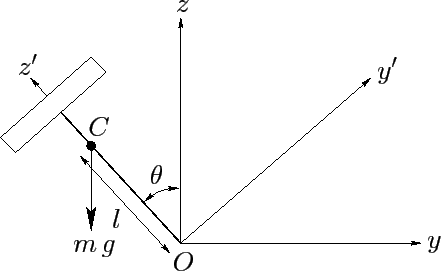
Let us now study the motion of a rigid rotationally symmetric top which
is free to turn about a fixed point (without friction), but which is
subject to a gravitational torque--see Figure 30. Suppose that the 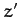 -axis
coincides with the symmetry axis. Let the principal moment of inertia about the symmetry axis
be
-axis
coincides with the symmetry axis. Let the principal moment of inertia about the symmetry axis
be  , and let the other principal moments both take the value
, and let the other principal moments both take the value 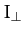 .
Suppose that the
.
Suppose that the
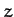 -axis points vertically upward, and let the common origin,
-axis points vertically upward, and let the common origin, 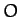 , of the
fixed and body frames coincide with the fixed point about which the top
turns. Suppose that
the center of mass of the top lies a distance
, of the
fixed and body frames coincide with the fixed point about which the top
turns. Suppose that
the center of mass of the top lies a distance 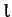 along its symmetry axis from point
along its symmetry axis from point 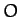 , and
that the mass of the top is
, and
that the mass of the top is  . Let the symmetry axis of the
top subtend an angle
. Let the symmetry axis of the
top subtend an angle 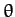 (which is an Eulerian angle) with
the upward vertical.
(which is an Eulerian angle) with
the upward vertical.
Figure 30:
A symmetric top.
 |
Consider an instant in time at which the Eulerian angle 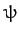 is zero.
This implies that the
is zero.
This implies that the 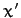 -axis is horizontal [see Equation (534)], as shown in the diagram.
The gravitational force, which acts at the
center of mass, thus exerts a torque
-axis is horizontal [see Equation (534)], as shown in the diagram.
The gravitational force, which acts at the
center of mass, thus exerts a torque
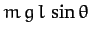 in the
in the
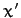 -direction. Hence, the components of the torque in the body
frame are
-direction. Hence, the components of the torque in the body
frame are
The components of the angular velocity vector in the body frame
are given by Equations (537)-(539).
Thus, Euler's equations
(504)-(506) take the form:
where
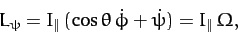 |
(562) |
and
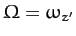 is the angular velocity of the top.
Multiplying Equation (560) by
is the angular velocity of the top.
Multiplying Equation (560) by 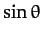 , we obtain
, we obtain
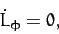 |
(563) |
where
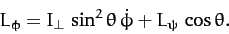 |
(564) |
According to Equations (561) and (563), the
two quantities  and
and 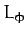 are constants
of the motion. These two quantities are the angular momenta of the
system about the
are constants
of the motion. These two quantities are the angular momenta of the
system about the 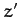 - and
- and 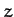 -axis, respectively. (To be more exact,
they are the generalized momenta conjugate to the coordinates
-axis, respectively. (To be more exact,
they are the generalized momenta conjugate to the coordinates 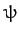 and
and
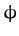 , respectively--see Section 9.8.) They
are conserved because the gravitational torque has no component
along either the
, respectively--see Section 9.8.) They
are conserved because the gravitational torque has no component
along either the 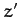 - or the
- or the 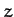 -axis. (Alternatively, they are
conserved because the Lagrangian of the top does not depend explicitly
on the coordinates
-axis. (Alternatively, they are
conserved because the Lagrangian of the top does not depend explicitly
on the coordinates 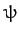 and
and 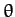 --see Section 9.8.)
--see Section 9.8.)
If there are no frictional forces acting on the top then the total
energy, 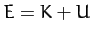 , is also a constant of the motion. Now,
, is also a constant of the motion. Now,
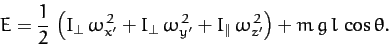 |
(565) |
When written in terms of the Eulerian angles (with 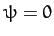 ), this
becomes
), this
becomes
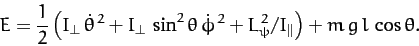 |
(566) |
Eliminating  between Equations (564) and (566),
we obtain the following differential equation for
between Equations (564) and (566),
we obtain the following differential equation for 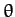 :
:
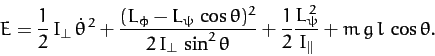 |
(567) |
Let
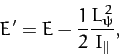 |
(568) |
and 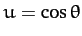 . It follows that
. It follows that
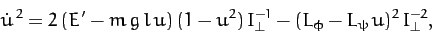 |
(569) |
or
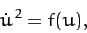 |
(570) |
where 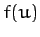 is a cubic polynomial. In principal, the above equation
can be integrated to give
is a cubic polynomial. In principal, the above equation
can be integrated to give  (and, hence,
(and, hence, 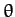 ) as a function of
) as a function of 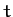 :
:
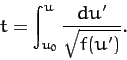 |
(571) |
Fortunately, we do not have to perform the above integration (which is very ugly)
in order to discuss the general properties of the solution to
Equation (570). It is clear, from Equation (571), that 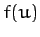 needs to be positive in order to obtain a physical solution. Hence, the
limits of the motion in
needs to be positive in order to obtain a physical solution. Hence, the
limits of the motion in 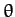 are determined by the three roots of the
equation
are determined by the three roots of the
equation 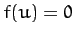 . Since
. Since 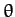 must lie between
must lie between  and
and  ,
it follows that
,
it follows that  must lie between 0 and 1. It can easily be demonstrated that
must lie between 0 and 1. It can easily be demonstrated that
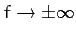 as
as
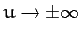 . It can also be shown
that the
largest root
. It can also be shown
that the
largest root 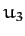 lies in the region
lies in the region 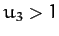 , and the two smaller
roots
, and the two smaller
roots 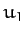 and
and 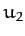 (if they exist) lie in the region
(if they exist) lie in the region
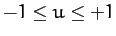 .
It follows that, in the region
.
It follows that, in the region
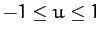 ,
, 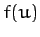 is only positive between
is only positive between 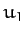 and
and 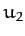 .
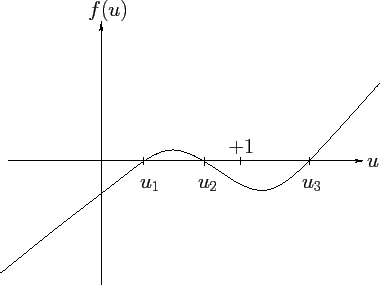
Figure 31 shows
a case where
.
Figure 31 shows
a case where 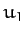 and
and 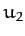 lie in the range
0 to 1. The corresponding values of
lie in the range
0 to 1. The corresponding values of 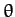 --
-- and
and 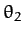 , say--are then the limits of the vertical motion.
The axis of the top oscillates backward and forward between these two
values of
, say--are then the limits of the vertical motion.
The axis of the top oscillates backward and forward between these two
values of 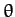 as the top precesses about the vertical axis. This
oscillation is called nutation. Incidentally, if
as the top precesses about the vertical axis. This
oscillation is called nutation. Incidentally, if 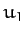 becomes
negative then the nutation will cause the top to strike the ground (assuming
that it is spinning on a level surface).
becomes
negative then the nutation will cause the top to strike the ground (assuming
that it is spinning on a level surface).
Figure 31:
The function 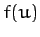 .
.
 |
If there is a double root of 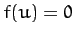 (i.e., if
(i.e., if  ) then
there is no nutation, and the top precesses steadily. However, the
criterion for steady precession is most easily obtained directly from
Equation (559). In the absence of nutation,
) then
there is no nutation, and the top precesses steadily. However, the
criterion for steady precession is most easily obtained directly from
Equation (559). In the absence of nutation,
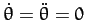 .
Hence, we obtain
.
Hence, we obtain
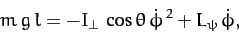 |
(572) |
or
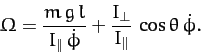 |
(573) |
The above equation is the criterion for steady precession.
Since the right-hand side of Equation (573) possesses a minimum
value, which is given by
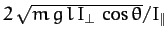 , it follows that
, it follows that
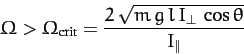 |
(574) |
is a necessary condition for obtaining steady precession at the
inclination angle 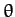 . For
. For
 , there are two
roots to Equation (573), corresponding to a slow and a fast steady
precession rate for a given inclination angle
, there are two
roots to Equation (573), corresponding to a slow and a fast steady
precession rate for a given inclination angle 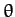 . If
. If
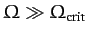 then these two roots are approximately given by
then these two roots are approximately given by
The slower of these two precession rates is the one which is
generally observed.



Next: Rotational Stability
Up: Rigid Body Rotation
Previous: Eulerian Angles
Richard Fitzpatrick
2011-03-31

![]() is zero.
This implies that the
is zero.
This implies that the ![]() -axis is horizontal [see Equation (534)], as shown in the diagram.
The gravitational force, which acts at the
center of mass, thus exerts a torque
-axis is horizontal [see Equation (534)], as shown in the diagram.
The gravitational force, which acts at the
center of mass, thus exerts a torque
![]() in the
in the
![]() -direction. Hence, the components of the torque in the body
frame are
-direction. Hence, the components of the torque in the body
frame are
![]() , is also a constant of the motion. Now,
, is also a constant of the motion. Now,
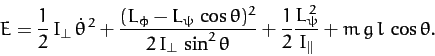
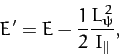
![]() needs to be positive in order to obtain a physical solution. Hence, the
limits of the motion in
needs to be positive in order to obtain a physical solution. Hence, the
limits of the motion in ![]() are determined by the three roots of the
equation
are determined by the three roots of the
equation ![]() . Since
. Since ![]() must lie between
must lie between ![]() and
and ![]() ,
it follows that
,
it follows that ![]() must lie between 0 and 1. It can easily be demonstrated that
must lie between 0 and 1. It can easily be demonstrated that
![]() as
as
![]() . It can also be shown
that the
largest root
. It can also be shown
that the
largest root ![]() lies in the region
lies in the region ![]() , and the two smaller
roots
, and the two smaller
roots ![]() and
and ![]() (if they exist) lie in the region
(if they exist) lie in the region
![]() .
It follows that, in the region
.
It follows that, in the region
![]() ,
, ![]() is only positive between
is only positive between ![]() and
and ![]() .
Figure 31 shows
a case where
.
Figure 31 shows
a case where ![]() and
and ![]() lie in the range
0 to 1. The corresponding values of
lie in the range
0 to 1. The corresponding values of ![]() --
--![]() and
and ![]() , say--are then the limits of the vertical motion.
The axis of the top oscillates backward and forward between these two
values of
, say--are then the limits of the vertical motion.
The axis of the top oscillates backward and forward between these two
values of ![]() as the top precesses about the vertical axis. This
oscillation is called nutation. Incidentally, if
as the top precesses about the vertical axis. This
oscillation is called nutation. Incidentally, if ![]() becomes
negative then the nutation will cause the top to strike the ground (assuming
that it is spinning on a level surface).
becomes
negative then the nutation will cause the top to strike the ground (assuming
that it is spinning on a level surface).
![]() (i.e., if
(i.e., if ![]() ) then
there is no nutation, and the top precesses steadily. However, the
criterion for steady precession is most easily obtained directly from
Equation (559). In the absence of nutation,
) then
there is no nutation, and the top precesses steadily. However, the
criterion for steady precession is most easily obtained directly from
Equation (559). In the absence of nutation,
![]() .
Hence, we obtain
.
Hence, we obtain