


Next: Scattering in the Center
Up: Two-Body Dynamics
Previous: Reduced Mass
Binary Star Systems
Approximately half of the stars in our galaxy are members of so-called binary star
systems. Such systems consist of two stars orbiting about their common
center of mass. The distance separating the stars is always much less than
the distance to the nearest neighbour star. Hence, a binary star system
can be treated as a two-body dynamical system to a very good approximation.
In a binary star system, the gravitational force which the first star exerts on
the second is
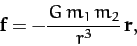 |
(329) |
where
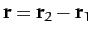 .
As we have seen, a two-body system can be reduced to an equivalent
one-body system whose equation of motion is of the form (327),
where
.
As we have seen, a two-body system can be reduced to an equivalent
one-body system whose equation of motion is of the form (327),
where
 .
Hence, in this particular case, we can write
.
Hence, in this particular case, we can write
 |
(330) |
which gives
 |
(331) |
where
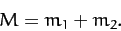 |
(332) |
Equation (331) is identical to Equation (212), which we have already
solved. Hence, we can immediately write down the solution:
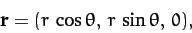 |
(333) |
where
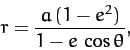 |
(334) |
and
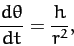 |
(335) |
with
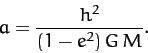 |
(336) |
Here, 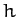 is a constant, and we have aligned our Cartesian axes so that the plane of the orbit
coincides with the
is a constant, and we have aligned our Cartesian axes so that the plane of the orbit
coincides with the 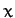 -
-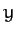 plane.
According to the above solution, the second star executes a Keplerian
elliptical orbit, with major radius
plane.
According to the above solution, the second star executes a Keplerian
elliptical orbit, with major radius  and eccentricity
and eccentricity 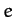 ,
relative to the first star, and vice versa. From Equation (258), the period of revolution,
,
relative to the first star, and vice versa. From Equation (258), the period of revolution, 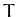 , is given by
, is given by
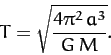 |
(337) |
In the inertial frame of reference whose origin always coincides with the center of mass--the so-called center of mass frame--the position vectors of the two stars are
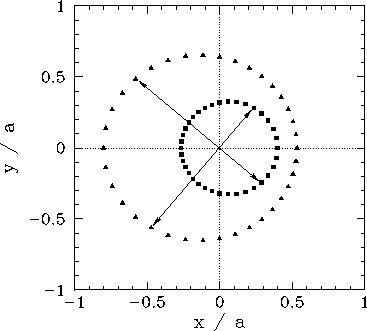
where  is specified above. Figure 20 shows an example binary star orbit, in the center of mass frame, calculated with
is specified above. Figure 20 shows an example binary star orbit, in the center of mass frame, calculated with 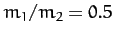 and
and 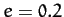 . Here, the triangles and squares denote the positions of the
first and second star, respectively (which are always diagrammatically opposite one another, as indicated by the arrows). It can be seen that both stars execute
elliptical orbits about their common center of mass.
. Here, the triangles and squares denote the positions of the
first and second star, respectively (which are always diagrammatically opposite one another, as indicated by the arrows). It can be seen that both stars execute
elliptical orbits about their common center of mass.
Figure 20:
An example binary star orbit.
 |
Binary star systems have been very useful to astronomers, since it is
possible to determine the masses of both stars in such a system
by careful observation.
The sum of the masses of the two stars, 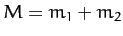 , can be found
from Equation (337) after a measurement of the major radius,
, can be found
from Equation (337) after a measurement of the major radius,  (which
is the mean of the greatest and smallest distance apart of the two
stars during their orbit), and the orbital period,
(which
is the mean of the greatest and smallest distance apart of the two
stars during their orbit), and the orbital period, 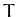 . The ratio of the
masses of the two stars,
. The ratio of the
masses of the two stars, 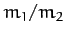 , can be determined from Equations (338) and (339) by
observing the fixed ratio of the relative distances of the two stars from the common
center of mass about which they both appear to rotate. Obviously, given the sum
of the masses, and the ratio of the masses, the individual masses themselves can
then be calculated.
, can be determined from Equations (338) and (339) by
observing the fixed ratio of the relative distances of the two stars from the common
center of mass about which they both appear to rotate. Obviously, given the sum
of the masses, and the ratio of the masses, the individual masses themselves can
then be calculated.



Next: Scattering in the Center
Up: Two-Body Dynamics
Previous: Reduced Mass
Richard Fitzpatrick
2011-03-31

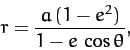
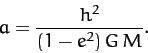
![]() , can be found
from Equation (337) after a measurement of the major radius,
, can be found
from Equation (337) after a measurement of the major radius, ![]() (which
is the mean of the greatest and smallest distance apart of the two
stars during their orbit), and the orbital period,
(which
is the mean of the greatest and smallest distance apart of the two
stars during their orbit), and the orbital period, ![]() . The ratio of the
masses of the two stars,
. The ratio of the
masses of the two stars, ![]() , can be determined from Equations (338) and (339) by
observing the fixed ratio of the relative distances of the two stars from the common
center of mass about which they both appear to rotate. Obviously, given the sum
of the masses, and the ratio of the masses, the individual masses themselves can
then be calculated.
, can be determined from Equations (338) and (339) by
observing the fixed ratio of the relative distances of the two stars from the common
center of mass about which they both appear to rotate. Obviously, given the sum
of the masses, and the ratio of the masses, the individual masses themselves can
then be calculated.