


Next: Perturbed Lunar Motion
Up: Lunar Motion
Previous: Lunar Equations of Motion
Let us, first of all, neglect the perturbing influence of the Sun on the Moon's orbit by setting 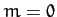 in the lunar equations of motion (1151)-(1153). For the sake of simplicity, let us also neglect nonlinear effects in these equations by setting
in the lunar equations of motion (1151)-(1153). For the sake of simplicity, let us also neglect nonlinear effects in these equations by setting
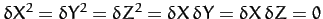 . In this case, the equations reduce to
. In this case, the equations reduce to
By inspection, appropriate solutions are
where 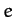 ,
, 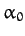 ,
, 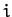 , and
, and 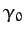 are arbitrary constants. Recalling that
are arbitrary constants. Recalling that 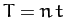 , it follows from (1154)-(1156)
that
, it follows from (1154)-(1156)
that
However, Equations (1163) and (1164) are simply first-order (in 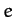 ) approximations to the
familiar Keplerian laws (see Chapter 5)
) approximations to the
familiar Keplerian laws (see Chapter 5)
where
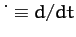 .
Of course, the above two laws describe a body
which executes an elliptical orbit, confocal with the Earth, of major radius
.
Of course, the above two laws describe a body
which executes an elliptical orbit, confocal with the Earth, of major radius  , mean angular velocity
, mean angular velocity  , and eccentricity
, and eccentricity
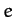 , such that the radius vector connecting the body to the Earth sweeps out equal areas in equal time intervals.
We conclude, unsurprisingly, that the unperturbed lunar orbit is a Keplerian ellipse.
Note that the lunar perigee lies at the fixed ecliptic longitude
, such that the radius vector connecting the body to the Earth sweeps out equal areas in equal time intervals.
We conclude, unsurprisingly, that the unperturbed lunar orbit is a Keplerian ellipse.
Note that the lunar perigee lies at the fixed ecliptic longitude
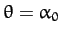 . Equation (1165) is the first-order approximation to
. Equation (1165) is the first-order approximation to
 |
(1168) |
This expression implies that the unperturbed lunar orbit is co-planar, but is inclined at an angle 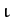 to the ecliptic plane.
Moreover, the ascending node lies at the fixed ecliptic longitude
to the ecliptic plane.
Moreover, the ascending node lies at the fixed ecliptic longitude
 . Incidentally, the neglect of nonlinear terms in Equations (1157)-(1159) is only valid as long as
. Incidentally, the neglect of nonlinear terms in Equations (1157)-(1159) is only valid as long as 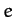 ,
, 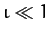 : i.e., provided that the unperturbed lunar orbit is only
slightly elliptical, and slightly inclined to the ecliptic plane. In fact, the observed values of
: i.e., provided that the unperturbed lunar orbit is only
slightly elliptical, and slightly inclined to the ecliptic plane. In fact, the observed values of 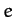 and
and
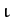 are
are 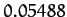 and
and  radians, respectively, so this is indeed the case.
radians, respectively, so this is indeed the case.



Next: Perturbed Lunar Motion
Up: Lunar Motion
Previous: Lunar Equations of Motion
Richard Fitzpatrick
2011-03-31
