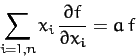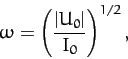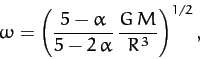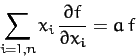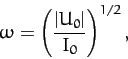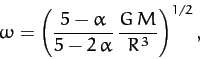Next: One-Dimensional Motion
Up: Newton's Laws of Motion
Previous: Non-Isolated Systems
- Consider an isolated system of
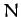 point objects interacting via
gravity. Let the mass and position vector of the
point objects interacting via
gravity. Let the mass and position vector of the  th object be
th object be
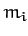 and
and 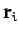 , respectively. What is the vector equation
of motion of the
, respectively. What is the vector equation
of motion of the  th object? Write expressions for the total
kinetic energy,
th object? Write expressions for the total
kinetic energy, 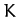 , and potential energy,
, and potential energy, 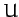 , of the system.
Demonstrate from the equations of motion that
, of the system.
Demonstrate from the equations of motion that 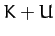 is a conserved quantity.
is a conserved quantity.
- Consider a function of many variables
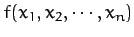 .
Such a function which satisfies
.
Such a function which satisfies
for all 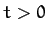 , and all values of the
, and all values of the 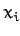 , is termed a homogenous function of degree
, is termed a homogenous function of degree 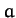 .
Prove the following theorem regarding homogeneous functions:
.
Prove the following theorem regarding homogeneous functions:
- Consider an isolated system of
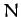 point objects interacting via
attractive central forces. Let the mass and position vector of the
point objects interacting via
attractive central forces. Let the mass and position vector of the  th object be
th object be
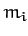 and
and 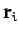 , respectively. Suppose that magnitude of the force exerted on object
, respectively. Suppose that magnitude of the force exerted on object  by
object
by
object 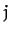 is
is
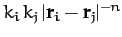 . Here, the
. Here, the 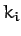 measure
some constant physical
property of the particles (e.g., their electric charges). Write
an expression for the total potential energy
measure
some constant physical
property of the particles (e.g., their electric charges). Write
an expression for the total potential energy 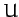 of the system. Is
this a homogenous function? If so, what is its degree?
Write the equation of motion of the
of the system. Is
this a homogenous function? If so, what is its degree?
Write the equation of motion of the  th particle. Use the mathematical
theorem from the previous exercise to demonstrate that
th particle. Use the mathematical
theorem from the previous exercise to demonstrate that
where
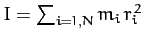 , and
, and 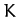 is the kinetic energy.
This result is known as the virial theorem.
Demonstrate that there are no bound steady-state equilibria for the system (i.e., states in which
the global system parameters do not evolve in time)
when
is the kinetic energy.
This result is known as the virial theorem.
Demonstrate that there are no bound steady-state equilibria for the system (i.e., states in which
the global system parameters do not evolve in time)
when 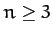 .
.
- A star can be through of as a spherical system that consists of a very large number of particles interacting
via gravity. Show that, for such a system, the virial theorem, introduced in the previous exercise, implies that
where 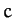 is a constant, and the
is a constant, and the 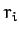 are measured from the geometric center. Hence, deduce that the angular frequency of small amplitude radial pulsations
of the star (in which the radial displacement is directly proportional to the radial distance from the center) takes the form
are measured from the geometric center. Hence, deduce that the angular frequency of small amplitude radial pulsations
of the star (in which the radial displacement is directly proportional to the radial distance from the center) takes the form
where 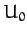 and
and 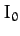 are the equilibrium values of
are the equilibrium values of 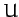 and
and 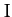 . Finally, show that if the mass
density within the star varies as
. Finally, show that if the mass
density within the star varies as 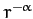 , where
, where 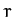 is the radial distance from the geometric center, and where
is the radial distance from the geometric center, and where 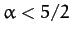 , then
, then
where 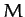 and
and 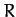 are the stellar mass and radius, respectively.
are the stellar mass and radius, respectively.
- Consider a system of
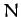 point particles. Let the
point particles. Let the  th particle have mass
th particle have mass 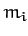 , electric
charge
, electric
charge 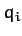 , and position vector
, and position vector 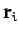 . Suppose that the charge to
mass ratio,
. Suppose that the charge to
mass ratio, 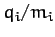 , is the same for all particles. The system is placed
in a uniform magnetic field
, is the same for all particles. The system is placed
in a uniform magnetic field 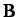 . Write the equation
of motion of the
. Write the equation
of motion of the  th particle. You may neglect any magnetic fields generated by the motion of the particles. Demonstrate that the total momentum
th particle. You may neglect any magnetic fields generated by the motion of the particles. Demonstrate that the total momentum
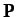 of the system precesses about
of the system precesses about 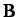 at the frequency
at the frequency
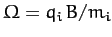 . Demonstrate that
. Demonstrate that
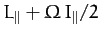 is a constant of the motion. Here,
is a constant of the motion. Here, 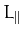 is the total angular momentum of the system parallel to the magnetic
field, and
is the total angular momentum of the system parallel to the magnetic
field, and 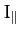 is the moment of inertia of the system about
an axis parallel to
is the moment of inertia of the system about
an axis parallel to 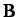 which passes through the origin.
which passes through the origin.



Next: One-Dimensional Motion
Up: Newton's Laws of Motion
Previous: Non-Isolated Systems
Richard Fitzpatrick
2011-03-31