


Next: Non-Isolated Systems
Up: Newton's Laws of Motion
Previous: Newton's Second Law of
Newton's Third Law of Motion
Consider a system of 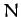 mutually interacting point objects.
Let the
mutually interacting point objects.
Let the  th object, whose mass is
th object, whose mass is 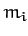 , be located at vector displacement
, be located at vector displacement 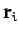 .
Suppose that this object exerts a force
.
Suppose that this object exerts a force 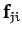 on the
on the 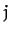 th object.
Likewise, suppose that the
th object.
Likewise, suppose that the 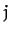 th object exerts a force
th object exerts a force 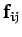 on the
on the
 th object.
Newton's third
law of motion essentially states that these two forces are equal and opposite, irrespective
of their nature.
In other words,
th object.
Newton's third
law of motion essentially states that these two forces are equal and opposite, irrespective
of their nature.
In other words,
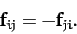 |
(23) |
One corollary of Newton's third law is that an object cannot exert
a force on itself. Another corollary is that all forces in the Universe have corresponding reactions. The only exceptions to this
rule are the fictitious forces which arise in non-inertial reference frames (e.g., the centrifugal and Coriolis
forces which appear in rotating reference frames--see Chapter 7). Fictitious forces do not possess reactions.
It should be noted that Newton's third law implies action at a
distance. In other words, if the force that object
 exerts on object
exerts on object 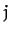 suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
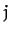 exerts on object
exerts on object  . Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's theory of relativity forbids information from traveling through the
Universe faster than the velocity of light in vacuum. Hence, action at a distance is also forbidden. In other words, if the force that object
. Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's theory of relativity forbids information from traveling through the
Universe faster than the velocity of light in vacuum. Hence, action at a distance is also forbidden. In other words, if the force that object
 exerts on object
exerts on object 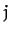 suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
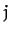 exerts on object
exerts on object  can respond. Of course, this means that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems on time-scales that are long compared to the time
required for light-rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
can respond. Of course, this means that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems on time-scales that are long compared to the time
required for light-rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
In an inertial frame, Newton's second law of motion applied to the  th object yields
th object yields
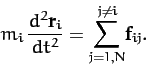 |
(24) |
Note that the summation on the right-hand side of the above equation excludes the case
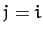 , since the
, since the  th object cannot exert a force on itself. Let us now take the above
equation and sum it over all objects. We obtain
th object cannot exert a force on itself. Let us now take the above
equation and sum it over all objects. We obtain
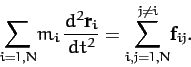 |
(25) |
Consider the sum over forces on the right-hand side of the above equation.
Each element of this sum--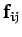 , say--can be paired with another element--
, say--can be paired with another element--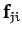 ,
in this case--which is equal and opposite, according to Newton's third law. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that the above equation can be written
,
in this case--which is equal and opposite, according to Newton's third law. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that the above equation can be written
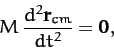 |
(26) |
where
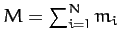 is the total mass. The quantity
is the total mass. The quantity 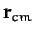 is the vector displacement of the center of mass of
the system, which is an imaginary point whose coordinates are the mass weighted
averages of the coordinates of the objects that constitute the system: i.e.,
is the vector displacement of the center of mass of
the system, which is an imaginary point whose coordinates are the mass weighted
averages of the coordinates of the objects that constitute the system: i.e.,
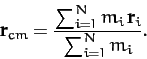 |
(27) |
According to Equation (26), the center of mass of the
system moves in a uniform straight-line, in accordance with
Newton's first law of motion, irrespective of the nature of the
forces acting between the various components of the system.
Now, if the center of mass moves in a uniform straight-line then
the center of mass velocity,
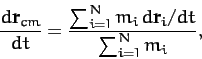 |
(28) |
is a constant of the motion. However, the momentum of the  th object takes the
form
th object takes the
form
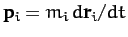 . Hence, the total momentum of the
system is written
. Hence, the total momentum of the
system is written
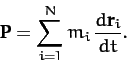 |
(29) |
A comparison of Equations (28) and (29) suggests that 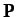 is also
a constant of the motion. In other words, the total momentum
of the system is a conserved quantity, irrespective of the nature of the
forces acting between the various components of the system. This result (which only holds if there is no net external force acting on the system) is
a direct consequence of Newton's third law of motion.
is also
a constant of the motion. In other words, the total momentum
of the system is a conserved quantity, irrespective of the nature of the
forces acting between the various components of the system. This result (which only holds if there is no net external force acting on the system) is
a direct consequence of Newton's third law of motion.
Taking the vector product of Equation (24) with the position vector 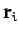 , we
obtain
, we
obtain
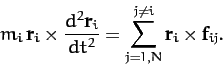 |
(30) |
However, it is easily seen that
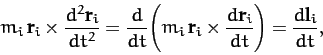 |
(31) |
where
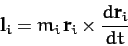 |
(32) |
is the angular momentum of the  th particle about the origin
of our coordinate system.
The total angular momentum of the system (about the origin) takes the form
th particle about the origin
of our coordinate system.
The total angular momentum of the system (about the origin) takes the form
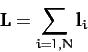 |
(33) |
Hence, summing Equation (30) over all particles, we obtain
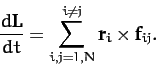 |
(34) |
Consider the sum on the right-hand side of the above equation. A general term,
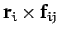 , in this sum can always be paired with a
matching term,
, in this sum can always be paired with a
matching term,
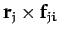 , in which the indices have been swapped.
Making use of Equation (23), the sum of a general matched pair can be written
, in which the indices have been swapped.
Making use of Equation (23), the sum of a general matched pair can be written
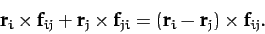 |
(35) |
Let us assume that the forces acting between the
various components of the system are central in nature, so
that 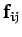 is parallel
to
is parallel
to
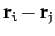 . In other words, the force exerted on object
. In other words, the force exerted on object 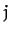 by object
by object  either points directly toward, or directly away from, object
either points directly toward, or directly away from, object  ,
and vice versa.
This is a reasonable assumption,
since most of the forces which we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the above expression is zero.
We conclude that
,
and vice versa.
This is a reasonable assumption,
since most of the forces which we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the above expression is zero.
We conclude that
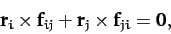 |
(36) |
for all values of  and
and  . Thus, the sum on the right-hand side of Equation (34) is zero for any kind of central force. We are left with
. Thus, the sum on the right-hand side of Equation (34) is zero for any kind of central force. We are left with
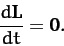 |
(37) |
In other words, the total angular momentum of the system is
a conserved quantity, provided that the different components of the
system interact via central forces (and there is no net external torque
acting on the system).



Next: Non-Isolated Systems
Up: Newton's Laws of Motion
Previous: Newton's Second Law of
Richard Fitzpatrick
2011-03-31
![]() exerts on object
exerts on object ![]() suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
![]() exerts on object
exerts on object ![]() . Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's theory of relativity forbids information from traveling through the
Universe faster than the velocity of light in vacuum. Hence, action at a distance is also forbidden. In other words, if the force that object
. Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's theory of relativity forbids information from traveling through the
Universe faster than the velocity of light in vacuum. Hence, action at a distance is also forbidden. In other words, if the force that object
![]() exerts on object
exerts on object ![]() suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
![]() exerts on object
exerts on object ![]() can respond. Of course, this means that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems on time-scales that are long compared to the time
required for light-rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
can respond. Of course, this means that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems on time-scales that are long compared to the time
required for light-rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
![]() th object yields
th object yields
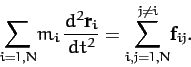
![]() , we
obtain
, we
obtain
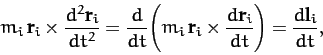
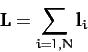
![]() , in this sum can always be paired with a
matching term,
, in this sum can always be paired with a
matching term,
![]() , in which the indices have been swapped.
Making use of Equation (23), the sum of a general matched pair can be written
, in which the indices have been swapped.
Making use of Equation (23), the sum of a general matched pair can be written