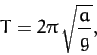Next: Potential Outside a Uniform
Up: Gravitational Potential Theory
Previous: Axially Symmetric Mass Distributions
Let us calculate the gravitational potential generated by a sphere of
uniform mass density 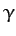 and radius
and radius  . Expressing
. Expressing
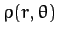 in the form (891), it is clear that
in the form (891), it is clear that
 |
(894) |
with 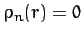 for
for 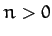 . Thus, from (893),
. Thus, from (893),
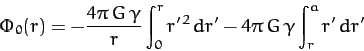 |
(895) |
for  , and
, and
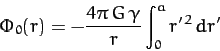 |
(896) |
for 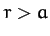 , with
, with 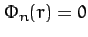 for
for 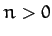 . Hence,
. Hence,
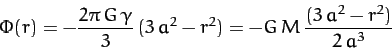 |
(897) |
for  , and
, and
 |
(898) |
for 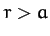 . Here,
. Here,
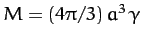 is the total mass of the sphere.
is the total mass of the sphere.
According to Equation (898), the gravitational potential outside a uniform sphere of mass 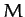 is the same as that generated by a point mass
is the same as that generated by a point mass 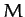 located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
previous analysis, it is clear that
located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
previous analysis, it is clear that
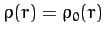 and
and
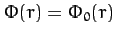 for a spherically symmetric mass distribution. Suppose that the mass
distribution extends out to
for a spherically symmetric mass distribution. Suppose that the mass
distribution extends out to 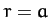 . It immediately follows, from Equation (893),
that
. It immediately follows, from Equation (893),
that
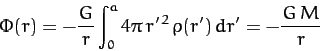 |
(899) |
for 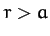 ,
where
,
where 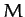 is the total mass of the distribution. We, thus, conclude that
Newton's laws of motion, in their primitive form, apply not only to
point masses, but also to extended spherically symmetric masses. In fact, this
is something which we have implicitly assumed all along in this book.
is the total mass of the distribution. We, thus, conclude that
Newton's laws of motion, in their primitive form, apply not only to
point masses, but also to extended spherically symmetric masses. In fact, this
is something which we have implicitly assumed all along in this book.
According to Equation (897), the gravitational potential inside a uniform
sphere is quadratic in 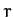 . This implies that if a narrow shaft were
drilled though the center of the sphere then a test mass,
. This implies that if a narrow shaft were
drilled though the center of the sphere then a test mass,  , moving in this
shaft would experience a gravitational force acting toward the
center which scales linearly in
, moving in this
shaft would experience a gravitational force acting toward the
center which scales linearly in 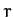 . In fact, the
force in question is given by
. In fact, the
force in question is given by
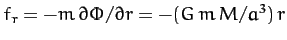 . It follows that a test mass dropped into the shaft executes simple
harmonic motion about the center of the sphere with period
. It follows that a test mass dropped into the shaft executes simple
harmonic motion about the center of the sphere with period
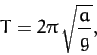 |
(900) |
where 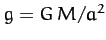 is the gravitational acceleration at the sphere's surface.
is the gravitational acceleration at the sphere's surface.



Next: Potential Outside a Uniform
Up: Gravitational Potential Theory
Previous: Axially Symmetric Mass Distributions
Richard Fitzpatrick
2011-03-31


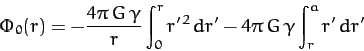
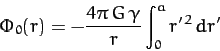
![]() is the same as that generated by a point mass
is the same as that generated by a point mass ![]() located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
previous analysis, it is clear that
located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
previous analysis, it is clear that
![]() and
and
![]() for a spherically symmetric mass distribution. Suppose that the mass
distribution extends out to
for a spherically symmetric mass distribution. Suppose that the mass
distribution extends out to ![]() . It immediately follows, from Equation (893),
that
. It immediately follows, from Equation (893),
that
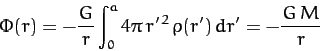
![]() . This implies that if a narrow shaft were
drilled though the center of the sphere then a test mass,
. This implies that if a narrow shaft were
drilled though the center of the sphere then a test mass, ![]() , moving in this
shaft would experience a gravitational force acting toward the
center which scales linearly in
, moving in this
shaft would experience a gravitational force acting toward the
center which scales linearly in ![]() . In fact, the
force in question is given by
. In fact, the
force in question is given by
![]() . It follows that a test mass dropped into the shaft executes simple
harmonic motion about the center of the sphere with period
. It follows that a test mass dropped into the shaft executes simple
harmonic motion about the center of the sphere with period