


Next: Axisymmetric Incompressible Inviscid Flow
Up: Two-Dimensional Potential Flow
Previous: Blasius Theorem
- Demonstrate that a line source of strength
 (running along the
(running along the  -axis) situated in a uniform flow of (unperturbed) velocity
-axis) situated in a uniform flow of (unperturbed) velocity 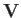 (lying in the
(lying in the  -
- plane) and density
plane) and density  experiences a force per unit length
experiences a force per unit length
- Demonstrate that a vortex filament of intensity
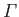 (running along the
(running along the  -axis) situated in a uniform flow of (unperturbed) velocity
-axis) situated in a uniform flow of (unperturbed) velocity 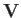 (lying in the
(lying in the  -
- plane) and density
plane) and density  experiences a force per unit length
experiences a force per unit length
- Show that two parallel line sources of strengths
 and
and 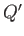 , located a perpendicular distance
, located a perpendicular distance  apart, exert a radial
force per unit length
apart, exert a radial
force per unit length
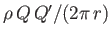 on one another, the force being attractive if
on one another, the force being attractive if  , and
repulsive if
, and
repulsive if 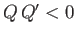 .
.
- Show that two parallel vortex filaments of intensities
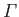 and
and
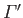 , located a perpendicular distance
, located a perpendicular distance  apart, exert a radial
force per unit length
apart, exert a radial
force per unit length
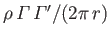 on one another, the force being repulsive if
on one another, the force being repulsive if
 , and
attractive if
, and
attractive if
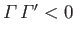 .
.
- A vortex filament of intensity
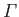 runs parallel to, and lies a perpendicular distance
runs parallel to, and lies a perpendicular distance  from, a rigid planar boundary. Demonstrate that
the boundary experiences a net force per unit length
from, a rigid planar boundary. Demonstrate that
the boundary experiences a net force per unit length
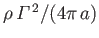 directed toward the
filament.
directed toward the
filament.
- Two rigid planar boundaries meet at right-angles. A line source of strength
 runs parallel to the line of intersection of the planes, and is situated a
perpendicular distance
runs parallel to the line of intersection of the planes, and is situated a
perpendicular distance  from each. Demonstrate that the source is subject to a force per unit length
from each. Demonstrate that the source is subject to a force per unit length
directed towards the line of intersection of the planes.
- A line source of strength
 is located a distance
is located a distance 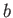 from an impenetrable circular cylinder of radius
from an impenetrable circular cylinder of radius 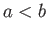 (the axis
of the cylinder being parallel to the source). Demonstrate that the cylinder experiences a net force per unit length
(the axis
of the cylinder being parallel to the source). Demonstrate that the cylinder experiences a net force per unit length
directed toward the source.
- A dipole line source consists of a line source of strength
 , running parallel to the
, running parallel to the  -axis, and intersecting the
-axis, and intersecting the  -
- plane at
plane at
 ,
,
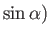 , and
a parallel source of strength
, and
a parallel source of strength  that intersects the
that intersects the  -
- plane at
plane at
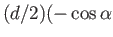 ,
,
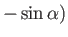 . Show
that, in the limit
. Show
that, in the limit
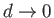 , and
, and
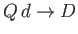 , the complex velocity potential of the source is
, the complex velocity potential of the source is
Here,
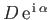 is termed the complex dipole strength.
is termed the complex dipole strength.
- A dipole line source of complex strength
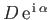 is placed in a uniformly flowing fluid
of speed
is placed in a uniformly flowing fluid
of speed 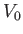 whose direction of motion subtends a (counter-clockwise) angle
whose direction of motion subtends a (counter-clockwise) angle  with the
with the  -axis.
Show that, while no net force acts on the source, it is subject to a moment (per unit length)
-axis.
Show that, while no net force acts on the source, it is subject to a moment (per unit length)
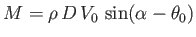 about the
about the
 -axis.
-axis.
- Consider a dipole line source of complex strength
 running along the
running along the  -axis,
and a second parallel source of complex strength
-axis,
and a second parallel source of complex strength
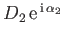 that intersects the
that intersects the  -
- plane
at
plane
at 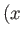 ,
,  .
Demonstrate that the first source is subject to a moment (per unit length) about the
.
Demonstrate that the first source is subject to a moment (per unit length) about the  -axis of
-axis of
as well as a force (per unit length) whose  - and
- and  -components are
-components are
respectively. Show that the second source is subject to the same moment, but an equal and opposite force.
- A dipole line source of complex strength
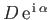 runs parallel to, and is located a
perpendicular distance
runs parallel to, and is located a
perpendicular distance  from, a rigid planar boundary. Show that the
boundary experiences a force per unit length
from, a rigid planar boundary. Show that the
boundary experiences a force per unit length
acting toward the source.
- Demonstrate that a conformal map converts a line source into a line source of the same strength, and
a vortex filament into a vortex filament of the same intensity.
- Consider the conformal map
where
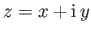 ,
,
 , and
, and 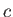 is real and positive. Show that
is real and positive. Show that
Demonstrate that 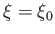 , where
, where
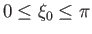 , maps to a circular arc of center
, maps to a circular arc of center 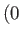 ,
,
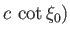 , and
radius
, and
radius
 , that connects the points
, that connects the points 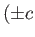 ,
,  , and lies in the region
, and lies in the region 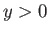 . Demonstrate that
. Demonstrate that
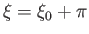 maps to the continuation of this arc in the region
maps to the continuation of this arc in the region 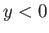 . In particular, show that
. In particular, show that 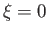 maps to the region
maps to the region 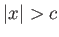 on the
on the  -axis, whereas
-axis, whereas 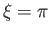 maps to the region
maps to the region 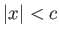 . Finally, show that
. Finally, show that
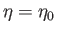 maps to a circle of center
maps to a circle of center
 ,
,  , and radius
, and radius
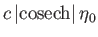 .
.
- Consider the complex velocity potential
where
Here, 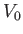 ,
, 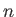 , and
, and 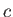 are real and positive. Show that
are real and positive. Show that
Hence, deduce that the flow at
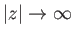 is uniform,
parallel to the
is uniform,
parallel to the  -axis, and of speed
-axis, and of speed 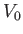 . Demonstrate that
. Demonstrate that
Hence, deduce that the streamline 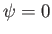 runs along the
runs along the  -axis for
-axis for 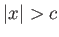 , but along a
circular arc connecting the points
, but along a
circular arc connecting the points 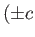 ,
,  for
for 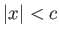 . Furthermore, show that if
. Furthermore, show that if 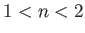 then this arc lies above the
then this arc lies above the
 -axis, and is of maximum height
-axis, and is of maximum height
but if 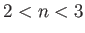 then the arc lies below the
then the arc lies below the  -axis, and is of maximum depth
-axis, and is of maximum depth
Hence, deduce that if 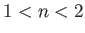 then the complex velocity potential under investigation corresponds to uniform flow of speed
then the complex velocity potential under investigation corresponds to uniform flow of speed 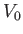 ,
parallel to a planar boundary that possesses
a cylindrical bump (whose axis is normal to the flow) of height
,
parallel to a planar boundary that possesses
a cylindrical bump (whose axis is normal to the flow) of height 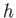 and width
and width 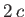 , but if
, but if 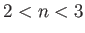 then the potential corresponds to flow parallel to a planar
boundary that possesses a cylindrical depression of depth
then the potential corresponds to flow parallel to a planar
boundary that possesses a cylindrical depression of depth  and width
and width 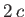 . Show, in particular, that if
. Show, in particular, that if  then
the bump is a half-cylinder, and if
then
the bump is a half-cylinder, and if  then the depression is a half-cylinder. Finally, demonstrate that the
flow speed at the top of the bump (in the case
then the depression is a half-cylinder. Finally, demonstrate that the
flow speed at the top of the bump (in the case 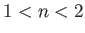 ), or the bottom of the depression (in the case
), or the bottom of the depression (in the case
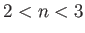 ) is
) is
- Show that
 maps the semi-infinite strip
maps the semi-infinite strip
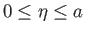 ,
, 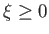 in the
in the 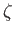 -plane
onto the upper half (
-plane
onto the upper half (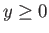 ) of the
) of the  -plane. Hence, show that the stream function due to a line source of strength
-plane. Hence, show that the stream function due to a line source of strength
 placed at
placed at
 ,
,  , in the rectangular region
, in the rectangular region
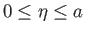 ,
, 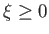 bounded by the rigid planes
bounded by the rigid planes
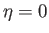 ,
, 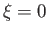 , and
, and 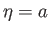 , is
, is
- Show that the complex velocity potential
can be interpreted as that due to uniform flow of speed 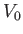 over a cylindrical log of radius
over a cylindrical log of radius  lying on the flat bed of a deep
stream (the axis of the log being normal to the flow).
Demonstrate that the flow speed at the top of the log is
lying on the flat bed of a deep
stream (the axis of the log being normal to the flow).
Demonstrate that the flow speed at the top of the log is
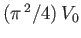 . Finally, show that the pressure
difference between the top and bottom of the log is
. Finally, show that the pressure
difference between the top and bottom of the log is
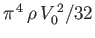 .
.
- Show that the complex potential
where
(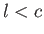 ) represents uniform flow of unperturbed speed
) represents uniform flow of unperturbed speed  , whose direction subtends a (counter-clockwise) angle
, whose direction subtends a (counter-clockwise) angle  with
the
with
the  -axis, around an impenetrable elliptic cylinder of major radius
-axis, around an impenetrable elliptic cylinder of major radius
 , aligned along the
, aligned along the  -axis, and
minor radius
-axis, and
minor radius
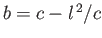 , aligned along the
, aligned along the  -axis. Demonstrate that the moment per unit length (about the
-axis. Demonstrate that the moment per unit length (about the  -axis)
exerted on the cylinder by the flow is
-axis)
exerted on the cylinder by the flow is
Hence, deduce that the moment acts to turn the cylinder broadside-on to the flow (i.e.,
 is a dynamically stable
equilibrium state), and that the equilibrium state in which the cylinder is aligned with the flow (i.e.,
is a dynamically stable
equilibrium state), and that the equilibrium state in which the cylinder is aligned with the flow (i.e.,  ) is
dynamically unstable.
) is
dynamically unstable.
- Consider a simply-connected region of a two-dimensional flow pattern bounded on the inside by the closed curve
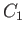 (lying in the
(lying in the  -
- plane), and on the
outside by the closed curve
plane), and on the
outside by the closed curve 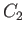 . Here,
. Here, 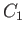 and
and 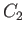 do not necessarily correspond to streamlines of the flow. Demonstrate that the kinetic energy per unit
length (in the
do not necessarily correspond to streamlines of the flow. Demonstrate that the kinetic energy per unit
length (in the  -direction) of the fluid lying between the two curves is
-direction) of the fluid lying between the two curves is
where  is the fluid mass density,
is the fluid mass density, 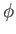 the velocity potential, and
the velocity potential, and  the stream function. Here,
the stream function. Here,  is a curve that runs from
is a curve that runs from 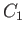 to
to 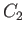 , and
, and ![$ [\phi]$](img2510.png) denotes the amount by which the velocity potential increases as the
argument of
denotes the amount by which the velocity potential increases as the
argument of
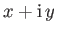 increases by
increases by  .
.
- Show that the complex potential
where
(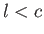 ) represents the flow pattern around an impenetrable elliptic cylinder of major radius
) represents the flow pattern around an impenetrable elliptic cylinder of major radius
 , aligned along the
, aligned along the  -axis, and
minor radius
-axis, and
minor radius
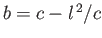 , aligned along the
, aligned along the  -axis, moving with speed
-axis, moving with speed  , in a direction that makes a counter-clockwise angle
, in a direction that makes a counter-clockwise angle  with the
with the  -axis, through a fluid that is at rest far from the cylinder. Demonstrate that the kinetic energy per unit length of the
flow pattern is
-axis, through a fluid that is at rest far from the cylinder. Demonstrate that the kinetic energy per unit length of the
flow pattern is
where  is the fluid mass density.
Hence, show that the cylinder's added mass per unit length is
is the fluid mass density.
Hence, show that the cylinder's added mass per unit length is
- Demonstrate from Equation (6.110) that the equation of the free streamline
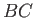 , in the case of a liquid jet emerging from
a two-dimensional orifice of semi-width
, in the case of a liquid jet emerging from
a two-dimensional orifice of semi-width  formed by a gap between two semi-infinite plane walls that subtend an angle
formed by a gap between two semi-infinite plane walls that subtend an angle 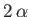 , can be written parametrically
as:
, can be written parametrically
as:
where
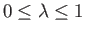 . Here, the orifice corresponds to the plane
. Here, the orifice corresponds to the plane  , and the flow a long way from the orifice is in the
, and the flow a long way from the orifice is in the 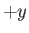 -direction.
Show that for the case of a two-dimensional Borda mouthpiece,
-direction.
Show that for the case of a two-dimensional Borda mouthpiece,
 , the previous equations reduce to
, the previous equations reduce to
Finally, show that the previous equations predict that the free streamline is re-entrant, with 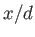 attaining its minimum value
attaining its minimum value
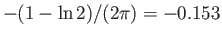 when
when
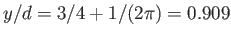 .
.



Next: Axisymmetric Incompressible Inviscid Flow
Up: Two-Dimensional Potential Flow
Previous: Blasius Theorem
Richard Fitzpatrick
2016-03-31
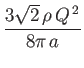
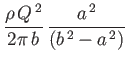
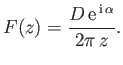
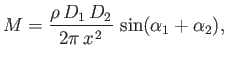
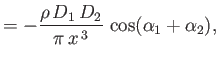
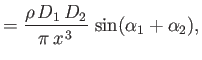

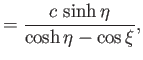
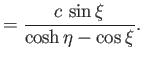
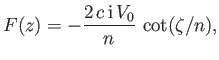

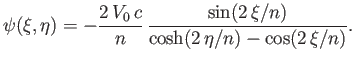
![$\displaystyle h = c\left[\frac{\cos(\pi\,n/2)+1}{\sin(\pi\,n/2)}\right],
$](img2484.png)
![$\displaystyle d = c\left[\frac{\cos(\pi\,n/2)+1}{\vert\sin(\pi\,n/2)\vert}\right].
$](img2486.png)
![$\displaystyle v = \frac{2\,V_0}{n^{\,2}}\left[1-\cos(\pi\,n/2)\right].
$](img2490.png)
![$\displaystyle \psi(\xi,\eta) = \frac{Q\,\sinh(\pi\,\xi/a)\,\sin(\pi\,\eta/a)}{2\pi\,[\sinh^2(\pi\,\xi/a)+\cos^2(\pi\,\eta/a)]}.
$](img2497.png)
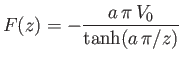
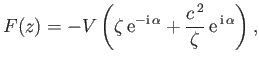
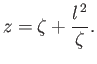

![$\displaystyle K= \frac{1}{2}\,\rho\left[\int_{C_2}\phi\,d\psi-\int_{C_1}\phi\,d\psi-\int_{C_3}[\phi]\,d\psi\right],
$](img2508.png)
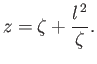
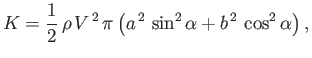
![$\displaystyle =\frac{2}{\pi}\int_{\sin^{-1}(\lambda)}^{\pi/2}\cos\left(\frac{2\...
...left(\frac{2\,\alpha}{\pi}\,\beta\right)\frac{d\beta}{\tan\beta}\right]^{\,-1},$](img2516.png)
![$\displaystyle =1-\frac{2}{\pi}\int_{\sin^{-1}(\lambda)}^{\pi/2}\sin\left(\frac{...
...left(\frac{2\,\alpha}{\pi}\,\beta\right)\frac{d\beta}{\tan\beta}\right]^{\,-1},$](img2517.png)
![$\displaystyle = \frac{1}{\pi}\left[-\ln(\lambda)-1+\lambda^{\,2}\right],$](img2519.png)
![$\displaystyle = \frac{1}{2}+\frac{1}{\pi}\left[\sin^{-1}(\lambda)+\lambda\,(1-\lambda^{\,2})^{1/2}\right].$](img2520.png)