


Next: Conservation Laws
Up: Mathematical Models of Fluid
Previous: Stress Tensor in a
The significance of the parameter 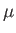 , appearing in the previous expression for the stress tensor, can be seen from the form taken by the relation (1.25) in the
special case of simple shearing motion. With
, appearing in the previous expression for the stress tensor, can be seen from the form taken by the relation (1.25) in the
special case of simple shearing motion. With
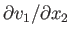 as the only non-zero
velocity derivative, all of the components of
as the only non-zero
velocity derivative, all of the components of 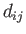 are zero apart from the
shear stresses
are zero apart from the
shear stresses
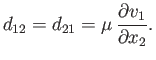 |
(1.27) |
Thus, 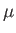 is the constant of proportionality between the rate of shear and the tangential
force per unit area when parallel plane layers of fluid slide over one another. This constant of proportionality is generally
referred to as viscosity. It is a matter of experience that the force acting between layers
of fluid undergoing relative sliding motion always tends to oppose
the motion, which implies that
is the constant of proportionality between the rate of shear and the tangential
force per unit area when parallel plane layers of fluid slide over one another. This constant of proportionality is generally
referred to as viscosity. It is a matter of experience that the force acting between layers
of fluid undergoing relative sliding motion always tends to oppose
the motion, which implies that 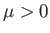 .
.
The viscosities of dry air and pure water at
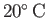 and atmospheric pressure are about
and atmospheric pressure are about
 and
and
 , respectively. In neither case does the viscosity exhibit
much variation with pressure. However, the viscosity of air increases by about
, respectively. In neither case does the viscosity exhibit
much variation with pressure. However, the viscosity of air increases by about 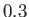 percent, and
that of water decreases by about 3 percent, per degree Centigrade
rise in temperature (Batchelor 2000).
percent, and
that of water decreases by about 3 percent, per degree Centigrade
rise in temperature (Batchelor 2000).



Next: Conservation Laws
Up: Mathematical Models of Fluid
Previous: Stress Tensor in a
Richard Fitzpatrick
2016-03-31
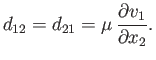
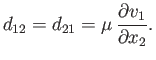
![]() and atmospheric pressure are about
and atmospheric pressure are about
![]() and
and
![]() , respectively. In neither case does the viscosity exhibit
much variation with pressure. However, the viscosity of air increases by about
, respectively. In neither case does the viscosity exhibit
much variation with pressure. However, the viscosity of air increases by about ![]() percent, and
that of water decreases by about 3 percent, per degree Centigrade
rise in temperature (Batchelor 2000).
percent, and
that of water decreases by about 3 percent, per degree Centigrade
rise in temperature (Batchelor 2000).