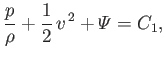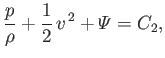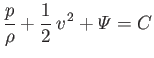Next: Euler Momentum Theorem
Up: Incompressible Inviscid Flow
Previous: Streamlines, Stream Tubes, and
Bernoulli's Theorem
In its most general form, Bernoulli's theorem--which was discovered by Daniel Bernoulli (1700-1783)--states that, in the steady flow of an inviscid fluid, the quantity
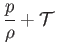 |
(4.2) |
is constant along a streamline, where  is the pressure,
is the pressure,  the density, and
the density, and 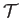 the total energy per unit mass.
the total energy per unit mass.
Figure 4.1:
Bernoulli's theorem.
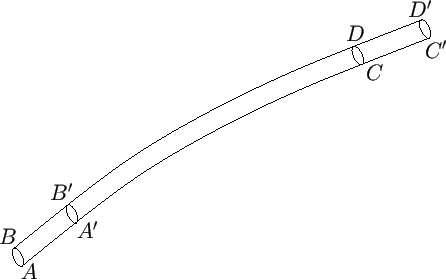 |
The proof is straightforward. Consider the body of fluid bounded by the cross-sectional areas 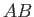 and
and 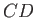 of the stream filament
pictured in Figure 4.1. Let us denote the values of quantities at
of the stream filament
pictured in Figure 4.1. Let us denote the values of quantities at 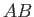 and
and 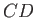 by the suffixes
by the suffixes 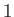 and
and
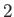 , respectively. Thus,
, respectively. Thus, 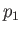 ,
,  ,
, 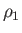 ,
, 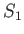 ,
,
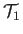 are the pressure, flow speed, mass density, cross-sectional
area, and total energy per unit mass, respectively, at
are the pressure, flow speed, mass density, cross-sectional
area, and total energy per unit mass, respectively, at 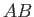 , et cetera. Suppose that, after a short time interval
, et cetera. Suppose that, after a short time interval 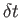 , the body of fluid has moved such
that it occupies the section of the filament bounded by the cross-sections
, the body of fluid has moved such
that it occupies the section of the filament bounded by the cross-sections  and
and 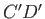 , where
, where
 and
and
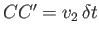 . Because the motion is steady, the mass
. Because the motion is steady, the mass 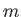 of the fluid between
of the fluid between 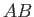 and
and  is the same as that between
is the same as that between 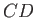 and
and 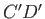 , so that
, so that
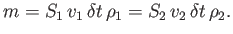 |
(4.3) |
Let 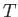 denote the total energy of the section of the fluid lying between
denote the total energy of the section of the fluid lying between  and
and 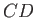 . Thus, the increase in energy
of the fluid body in the time interval
. Thus, the increase in energy
of the fluid body in the time interval 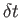 is
is
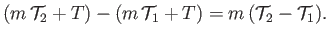 |
(4.4) |
In the absence of viscous energy dissipation, this energy increase must equal the net work done on the fluid by the pressures at
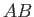 and
and 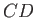 , which is
, which is
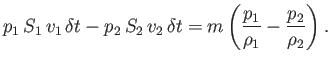 |
(4.5) |
Equating expressions (4.4) and (4.5), we find that
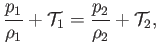 |
(4.6) |
which demonstrates that
 has the same value at any two points on a given stream filament, and is therefore constant along the filament. Note that Bernoulli's theorem has only been proved for the case of the steady motion of an inviscid fluid. However,
the fluid in question may either be compressible or incompressible.
has the same value at any two points on a given stream filament, and is therefore constant along the filament. Note that Bernoulli's theorem has only been proved for the case of the steady motion of an inviscid fluid. However,
the fluid in question may either be compressible or incompressible.
For the particular case of an incompressible fluid, moving in a conservative force-field, the total energy per unit mass is the
sum of the kinetic energy per unit mass,
 , and the potential energy per unit mass,
, and the potential energy per unit mass,
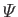 , and
Bernoulli's theorem thus becomes
, and
Bernoulli's theorem thus becomes
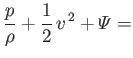 constant along a streamline constant along a streamline |
(4.7) |
If we focus on a particular streamline, 1 (say), then Bernoulli's theorem states that
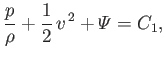 |
(4.8) |
where 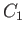 is a constant characterizing that streamline. If we consider a second streamline, 2 (say), then
is a constant characterizing that streamline. If we consider a second streamline, 2 (say), then
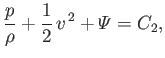 |
(4.9) |
where 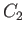 is another constant. It is not generally the case that
is another constant. It is not generally the case that 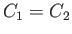 . If, however, the fluid motion is
irrotational then the constant in Bernoulli's theorem is the same for all streamlines (see Section 4.15), so
that
. If, however, the fluid motion is
irrotational then the constant in Bernoulli's theorem is the same for all streamlines (see Section 4.15), so
that
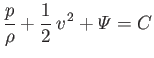 |
(4.10) |
throughout the fluid.



Next: Euler Momentum Theorem
Up: Incompressible Inviscid Flow
Previous: Streamlines, Stream Tubes, and
Richard Fitzpatrick
2016-03-31
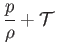
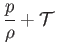
![]() and
and ![]() of the stream filament
pictured in Figure 4.1. Let us denote the values of quantities at
of the stream filament
pictured in Figure 4.1. Let us denote the values of quantities at ![]() and
and ![]() by the suffixes
by the suffixes ![]() and
and
![]() , respectively. Thus,
, respectively. Thus, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() are the pressure, flow speed, mass density, cross-sectional
area, and total energy per unit mass, respectively, at
are the pressure, flow speed, mass density, cross-sectional
area, and total energy per unit mass, respectively, at ![]() , et cetera. Suppose that, after a short time interval
, et cetera. Suppose that, after a short time interval ![]() , the body of fluid has moved such
that it occupies the section of the filament bounded by the cross-sections
, the body of fluid has moved such
that it occupies the section of the filament bounded by the cross-sections ![]() and
and ![]() , where
, where
![]() and
and
![]() . Because the motion is steady, the mass
. Because the motion is steady, the mass ![]() of the fluid between
of the fluid between ![]() and
and ![]() is the same as that between
is the same as that between ![]() and
and ![]() , so that
, so that
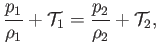
![]() , and the potential energy per unit mass,
, and the potential energy per unit mass,
![]() , and
Bernoulli's theorem thus becomes
, and
Bernoulli's theorem thus becomes
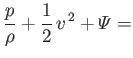 constant along a streamline
constant along a streamline