


Next: General Properties of Stress
Up: Mathematical Models of Fluid
Previous: What is a Fluid?
Volume and Surface Forces
Generally speaking, fluids are acted upon by two distinct types of force. The first type is long range in nature--that is, such that it decreases relatively slowly with increasing distance between interacting elements--and is
capable of completely penetrating into the interior of a fluid. Gravity
is an obvious example of a long-range force. One consequence of the relatively slow variation of
long-range forces with position is that they
act equally on all of the fluid contained within a sufficiently small volume element. In this situation, the net force
acting on the element becomes directly proportional to its volume. For this reason, long-range forces are often called volume forces. In the following, we shall write the total volume force acting at time 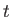 on the fluid contained within a
small volume element of magnitude
on the fluid contained within a
small volume element of magnitude  , centered on a fixed point whose position vector is
, centered on a fixed point whose position vector is  ,
as
,
as
 |
(1.1) |
The second type of force is short range in nature, and
is most conveniently modeled as momentum transport within the fluid. Such transport is generally due to a combination of
the mutual forces exerted by contiguous molecules, and momentum fluxes caused by relative molecular motion.
Suppose that
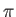
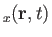 is the net flux density of
is the net flux density of  -directed fluid momentum due to
short-range forces
at position
-directed fluid momentum due to
short-range forces
at position  and time
and time 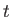 . In other words, suppose that, at position
. In other words, suppose that, at position  and
time
and
time 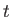 , as a direct consequence of short-range forces,
, as a direct consequence of short-range forces,  -momentum is flowing at the rate of
-momentum is flowing at the rate of
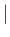
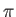
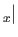 newton-seconds per meter squared per second in the direction of vector
newton-seconds per meter squared per second in the direction of vector
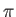
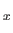 . Consider an infinitesimal plane surface element,
. Consider an infinitesimal plane surface element,
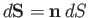 , located at point
, located at point  . Here,
. Here, 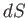 is the
area of the element, and
is the
area of the element, and 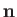 its unit normal. (See Section A.7.) The fluid which lies
on that side of the element toward which
its unit normal. (See Section A.7.) The fluid which lies
on that side of the element toward which 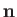 points is said to lie on its positive side, and vice versa.
The net flux of
points is said to lie on its positive side, and vice versa.
The net flux of  -momentum across the element (in the direction of
-momentum across the element (in the direction of 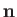 ) is
) is
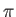
 newtons, which implies (from Newton's second law of motion) that the fluid on the positive side of the surface element
experiences a force
newtons, which implies (from Newton's second law of motion) that the fluid on the positive side of the surface element
experiences a force
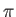
 in the
in the  -direction due to short-range
interaction with the fluid on the negative side.
According to Newton's third law of motion, the fluid on the negative side of the surface experiences a force
-direction due to short-range
interaction with the fluid on the negative side.
According to Newton's third law of motion, the fluid on the negative side of the surface experiences a force
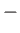
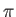
 in the
in the  -direction due to interaction with the fluid on the positive side.
Short-range forces
are often called surface forces, because they are directly proportional to the area of the surface element across which
they act.
Let
-direction due to interaction with the fluid on the positive side.
Short-range forces
are often called surface forces, because they are directly proportional to the area of the surface element across which
they act.
Let
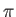
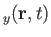 and
and
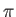
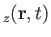 be the net flux density of
be the net flux density of  - and
- and  -momentum, respectively, at position
-momentum, respectively, at position  and
time
and
time 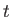 . By a straightforward extension of previous argument, the net surface force exerted by the fluid on the positive side of some
planar surface element,
. By a straightforward extension of previous argument, the net surface force exerted by the fluid on the positive side of some
planar surface element, 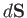 , on the fluid
on its negative side is
, on the fluid
on its negative side is
In tensor notation (see Appendix B), the previous equation can be written
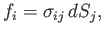 |
(1.3) |
where
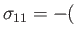
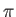
 ,
,
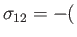
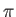
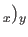 ,
,
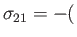
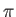
 , et cetera.
(Note that, because the subscript
, et cetera.
(Note that, because the subscript  is repeated in the previous equation, it is assumed to be summed from
is repeated in the previous equation, it is assumed to be summed from 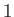 to
to  . Hence,
. Hence,
 is shorthand for
is shorthand for
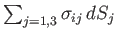 .)
Here, the
.)
Here, the
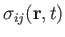 are termed the local stresses in the fluid at position
are termed the local stresses in the fluid at position  and
time
and
time 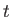 , and have units of force per unit area. Moreover, the
, and have units of force per unit area. Moreover, the
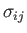 are
the components of a second-order tensor (see Appendix B) known as the stress tensor. [This follows because the
are
the components of a second-order tensor (see Appendix B) known as the stress tensor. [This follows because the 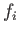 are the components of a first-order tensor (as all forces are proper vectors), and the
are the components of a first-order tensor (as all forces are proper vectors), and the 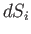 are the components of an arbitrary first-order tensor (as surface elements are
also proper vectors--see Section A.7--and Equation (1.3) holds for
surface elements whose normals point in any direction), so application of the quotient rule (see Section B.3) to Equation (1.3) reveals that the
are the components of an arbitrary first-order tensor (as surface elements are
also proper vectors--see Section A.7--and Equation (1.3) holds for
surface elements whose normals point in any direction), so application of the quotient rule (see Section B.3) to Equation (1.3) reveals that the
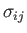 transform under rotation of the coordinate axes as the components of a second-order tensor.] We can interpret
transform under rotation of the coordinate axes as the components of a second-order tensor.] We can interpret
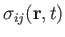 as the
as the 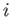 -component of the force per unit area exerted, at position
-component of the force per unit area exerted, at position  and time
and time 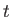 , across a plane surface element normal to the
, across a plane surface element normal to the
 -direction. The three diagonal components of
-direction. The three diagonal components of
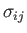 are
termed normal stresses, because each of them gives the normal component of the force per unit area acting
across a plane surface element parallel to one of the Cartesian coordinate planes. The six non-diagonal components
are termed shear stresses, because they drive shearing motion in which parallel
layers of fluid slide relative to one another.
are
termed normal stresses, because each of them gives the normal component of the force per unit area acting
across a plane surface element parallel to one of the Cartesian coordinate planes. The six non-diagonal components
are termed shear stresses, because they drive shearing motion in which parallel
layers of fluid slide relative to one another.



Next: General Properties of Stress
Up: Mathematical Models of Fluid
Previous: What is a Fluid?
Richard Fitzpatrick
2016-03-31
![]()
![]() is the net flux density of
is the net flux density of ![]() -directed fluid momentum due to
short-range forces
at position
-directed fluid momentum due to
short-range forces
at position ![]() and time
and time ![]() . In other words, suppose that, at position
. In other words, suppose that, at position ![]() and
time
and
time ![]() , as a direct consequence of short-range forces,
, as a direct consequence of short-range forces, ![]() -momentum is flowing at the rate of
-momentum is flowing at the rate of
![]()
![]()
![]() newton-seconds per meter squared per second in the direction of vector
newton-seconds per meter squared per second in the direction of vector
![]()
![]() . Consider an infinitesimal plane surface element,
. Consider an infinitesimal plane surface element,
![]() , located at point
, located at point ![]() . Here,
. Here, ![]() is the
area of the element, and
is the
area of the element, and ![]() its unit normal. (See Section A.7.) The fluid which lies
on that side of the element toward which
its unit normal. (See Section A.7.) The fluid which lies
on that side of the element toward which ![]() points is said to lie on its positive side, and vice versa.
The net flux of
points is said to lie on its positive side, and vice versa.
The net flux of ![]() -momentum across the element (in the direction of
-momentum across the element (in the direction of ![]() ) is
) is
![]()
![]() newtons, which implies (from Newton's second law of motion) that the fluid on the positive side of the surface element
experiences a force
newtons, which implies (from Newton's second law of motion) that the fluid on the positive side of the surface element
experiences a force
![]()
![]() in the
in the ![]() -direction due to short-range
interaction with the fluid on the negative side.
According to Newton's third law of motion, the fluid on the negative side of the surface experiences a force
-direction due to short-range
interaction with the fluid on the negative side.
According to Newton's third law of motion, the fluid on the negative side of the surface experiences a force
![]()
![]()
![]() in the
in the ![]() -direction due to interaction with the fluid on the positive side.
Short-range forces
are often called surface forces, because they are directly proportional to the area of the surface element across which
they act.
Let
-direction due to interaction with the fluid on the positive side.
Short-range forces
are often called surface forces, because they are directly proportional to the area of the surface element across which
they act.
Let
![]()
![]() and
and
![]()
![]() be the net flux density of
be the net flux density of ![]() - and
- and ![]() -momentum, respectively, at position
-momentum, respectively, at position ![]() and
time
and
time ![]() . By a straightforward extension of previous argument, the net surface force exerted by the fluid on the positive side of some
planar surface element,
. By a straightforward extension of previous argument, the net surface force exerted by the fluid on the positive side of some
planar surface element, ![]() , on the fluid
on its negative side is
, on the fluid
on its negative side is