Next: Analysis
Up: Ellipsoidal Potential Theory
Previous: Ellipsoidal Potential Theory
Let us adopt the right-handed Cartesian coordinate system 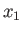 ,
, 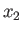 ,
, 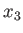 . Consider a homogeneous ellipsoidal body whose outer boundary
satisfies
. Consider a homogeneous ellipsoidal body whose outer boundary
satisfies
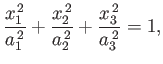 |
(D.1) |
where 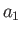 ,
, 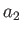 , and
, and 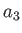 are the principal radii along the
are the principal radii along the 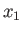 -,
-, 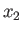 -, and
-, and 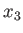 -axes, respectively.
Let us calculate the gravitational potential (i.e., the potential energy of a unit test mass) at some
point
-axes, respectively.
Let us calculate the gravitational potential (i.e., the potential energy of a unit test mass) at some
point
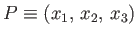 lying within this body. More information
on ellipsoidal potential theory can be found in Chandrasekhar 1969.
lying within this body. More information
on ellipsoidal potential theory can be found in Chandrasekhar 1969.
Richard Fitzpatrick
2016-03-31