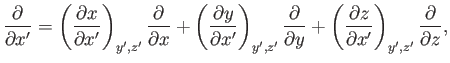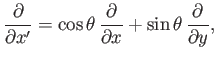Next: Divergence
Up: Vectors and Vector Fields
Previous: Gradient
Grad Operator
It is useful to define the vector operator
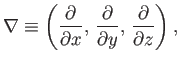 |
(A.119) |
which is usually called the grad or del operator.
This operator acts on everything to
its right in a expression, until the end of the expression
or a closing bracket is reached.
For instance,
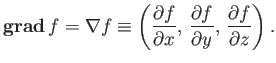 |
(A.120) |
For two scalar fields 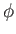 and
and 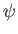 ,
,
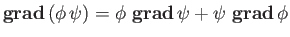 |
(A.121) |
can be written more succinctly as
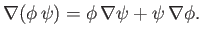 |
(A.122) |
Suppose that we rotate the coordinate axes through an angle 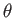 about
about 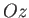 .
By analogy with Equations (A.17)-(A.19), the old coordinates (
.
By analogy with Equations (A.17)-(A.19), the old coordinates ( ,
,  ,
,  ) are related
to the new ones (
) are related
to the new ones (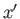 ,
, 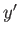 ,
, 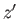 ) via
) via
Now,
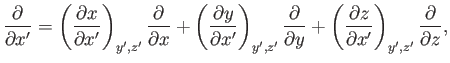 |
(A.126) |
giving
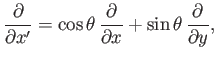 |
(A.127) |
and
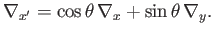 |
(A.128) |
It can be seen, from Equations (A.20)-(A.22), that
the differential operator  transforms in an analogous manner to
a vector.
This is another proof that
transforms in an analogous manner to
a vector.
This is another proof that 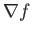 is a good vector.
is a good vector.



Next: Divergence
Up: Vectors and Vector Fields
Previous: Gradient
Richard Fitzpatrick
2016-03-31
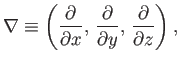
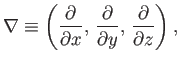
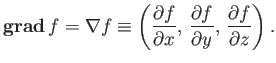
![]() about
about ![]() .
By analogy with Equations (A.17)-(A.19), the old coordinates (
.
By analogy with Equations (A.17)-(A.19), the old coordinates (![]() ,
, ![]() ,
, ![]() ) are related
to the new ones (
) are related
to the new ones (![]() ,
, ![]() ,
, ![]() ) via
) via