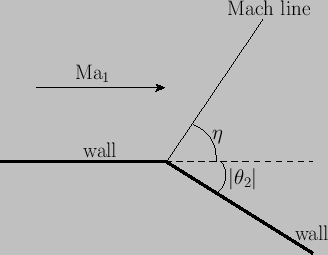
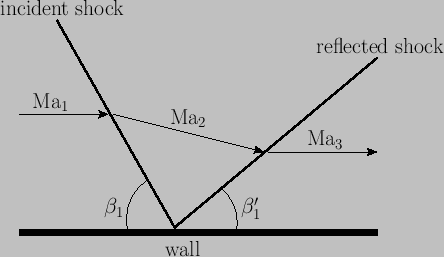
where
 |
||
![$\displaystyle = \frac{2\,{\rm Ma}_1^{\,2}+1}{{\rm Ma}_1^{\,4}}+\left[\left(\frac{\gamma+1}{2}\right)^2+\frac{\gamma-1}{{\rm Ma}_1^{\,2}}\right]\sin^2\theta,$](img6091.png) |
||
 |
Let
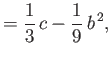 |
||
 |
||
Demonstrate that the oblique shock solution only exists for
 |
||
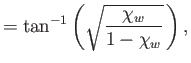 |
where
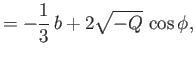 |
||
 |
||
![$\displaystyle = \frac{1}{3}\left[\tan^{-1}\left(\frac{\sqrt{-D}}{R}\right)+{\mit\Delta}\right].$](img6110.png) |
Here,
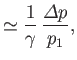 |
||
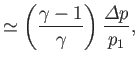 |
||
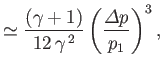 |
where

Here,
![$\displaystyle \frac{{\mit\Delta}{\rm Ma}}{{\rm Ma}_1}\simeq -\left[\frac{1+[(\gamma-1)/2]\,{\rm Ma}_1^{\,2}}{\sqrt{{\rm Ma}_1^{\,2}-1}}\right]\theta.
$](img6117.png)
where
![$\displaystyle \frac{{\mit\Delta}p}{p_1} \simeq \left(\frac{\gamma\,{\rm Ma}_1^{...
...\left[(\gamma+1)\,{\rm Ma}_1^{\,4}-4\,({\rm Ma}_1^{\,2}-1)\right]\theta^{\,2},
$](img6124.png)
where
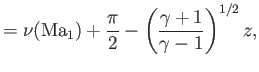 |
||
![$\displaystyle = \tan^{-1}\left[\left(\frac{\gamma-1}{\gamma+1}\right)^{1/2}({\rm Ma}_1^{\,2}-1)^{1/2}\right],$](img6129.png) |
where
![$\displaystyle = \cot^{-1}\left[({\rm Ma}_1^{\,2}-1)^{1/2}\,\frac{\tan z}{\tan z_1}\right],$](img6130.png) |
||
![$\displaystyle =\tan^{-1}\left[({\rm Ma}_1^{\,2}-1)^{1/2}\right] -\tan^{-1}\left...
...{\tan z}{\tan z_1}\right] +\left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}(z-z_1),$](img6132.png) |
||
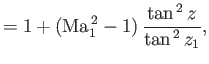 |
||
![$\displaystyle = \nu({\rm Ma}_1) +\tan^{-1}\left[({\rm Ma}_1^{\,2}-1)^{1/2}\righ...
...tan^{-1}\left[({\rm Ma}_1^{\,2}-1)^{1/2}\frac{\tan z}{\tan z_1}\right]\nonumber$](img6135.png) |
||
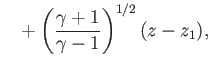 |
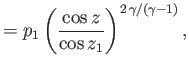 |
||
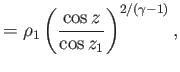 |
||
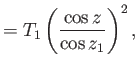 |
where
 |
Show that ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![$\displaystyle \nu\rightarrow\nu_{\rm max} \equiv \frac{\pi}{2}\left[\left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}-1\right],
$](img6150.png)
and
in the limit that
Assuming that
![]() , show that
, show that
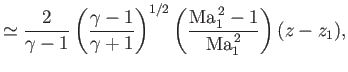 |
||
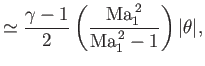 |
and
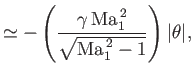 |
||
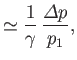 |
||
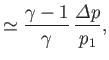 |
||
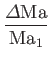 |
![$\displaystyle \simeq -\left(\frac{1+[(\gamma-1)/2]\,{\rm Ma}_1^{\,2}}{\gamma\,{\rm Ma}_1^{\,2}}\right)\frac{{\mit\Delta}p}{p_1},$](img6164.png) |
where
![$\displaystyle \frac{{\mit\Delta}p}{p_1} \simeq -\left(\frac{\gamma\,{\rm Ma}_1^...
...amma+1)\,{\rm Ma}_1^{\,4}-4\,({\rm Ma}_1^{\,2}-1)\right]\vert\theta\vert^{\,2}
$](img6166.png)
for a weak Prandtl-Mayer fan. (See Exercise v.)
![$\displaystyle \beta_1'-\beta_1\simeq 2\left[\left(\frac{\gamma+1}{4}\right)\left(\frac{{\rm Ma}_1^{\,2}}{{\rm Ma}_1^{\,2}-1}\right)-1\right]\theta_1,
$](img6168.png)
where
![$\displaystyle \delta = \left[\frac{1+[(\gamma-1)/2]\,{\rm Ma}_1^{\,2}}{\sqrt{{\rm Ma}_1^{\,2}-1}}\right]\theta_1.
$](img6176.png)
 |
where
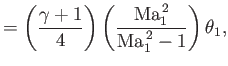 |
||
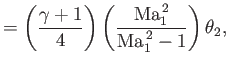 |
and
and also that
![$\displaystyle = \left[\frac{1+[(\gamma-1)/2]\,{\rm Ma}_1^{\,2}}{\sqrt{{\rm Ma}_1^{\,2}-1}}\right]\theta_1,$](img6187.png) |
||
![$\displaystyle = \left[\frac{1+[(\gamma-1)/2]\,{\rm Ma}_1^{\,2}}{\sqrt{{\rm Ma}_1^{\,2}-1}}\right]\theta_2.$](img6188.png) |
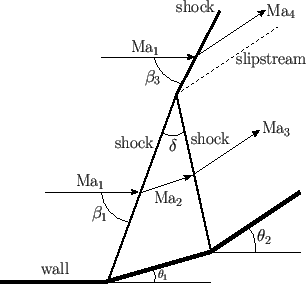
Demonstrate that the strength of the merged shock is approximately the sum of the strengths of the two component shocks, and, hence, that the pressures on either side of the slipstream shown in the figure are equal (at least, to first order in
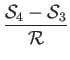 |
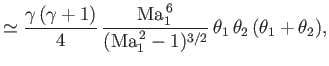 |
where
 |
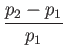 |
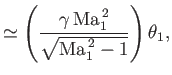 |
|
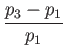 |
 |
|
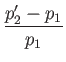 |
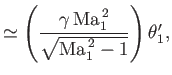 |
|
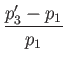 |
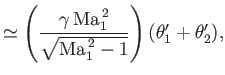 |
where
Show, that the respective strengths of the two shocks are unaffected by the intersection (at least, to first order in the deflection angles).
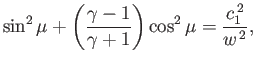
where
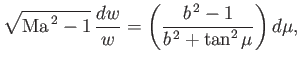
where

and, hence, that
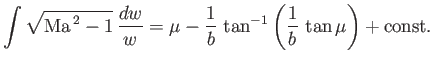
Finally, demonstrate that
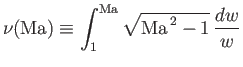 |
![$\displaystyle = \left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}\tan^{-1}\left(\lef...
...\frac{\gamma-1}{\gamma+1}\right)({\rm Ma}^{\,2}-1)\right]^{1/2}\right)\nonumber$](img6211.png) |
|
![$\displaystyle \phantom{=}-\tan^{-1}\left(\left[{\rm Ma}^{\,2}-1\right]^{1/2}\right).$](img6212.png) |
(Leipmann & Roshko 1957.)
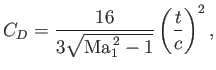
where
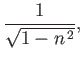
where
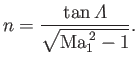
Here,
![$\displaystyle \phi(x,y) = \frac{U\,\epsilon}{m}\,\cos(\alpha\,x)\,\frac{\cosh[m\,\alpha\,(b-y)]}{\sinh(m\,\alpha\,b)}.
$](img6218.png)
Show, on the other hand, that if the flow is bounded by a free surface at
![$\displaystyle \phi(x,y) = \frac{U\,\epsilon}{m}\,\cos(\alpha\,x)\,\frac{\sinh[m\,\alpha\,(b-y)]}{\cosh(m\,\alpha\,b)}.
$](img6220.png)
(Leipmann & Roshko 1957.)