


Next: Detached Shocks
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Compression by Turning
Supersonic Expansion by Turning
Up to now, we have only considered turns that are concave. That is, turns in which the wall is deflected into the oncoming flow.
Let us now consider what happens in a convex turn, where the wall is deflected away from the oncoming flow. In particular, let
us investigate supersonic flow over a convex corner, such as that illustrated in Figure 15.8(a).
A convex turn through a single oblique shock, like that illustrated in Figure 15.8(a), is not possible. In such a turn, the deviation of the flow,
as it passes through shock, is inevitably away from the plane of the shock front. Such a deviation would require the downstream normal
flow speed to exceed the upstream normal flow speed (because the upstream and downstream tangential flow speeds are
equal). (See Section 15.2.) However, although this would satisfy the equations of fluid motion, it would lead to
a spontaneous decrease in specific entropy across the shock front, and is, thus, forbidden by the second law of thermodynamics. (See Section 14.8.)
What actually happens is as follows. The nonlinear mechanism that tends to steepen a compression (see Sections 14.4 and 15.5)
produces the opposite effect in an expansion. In particular, instead of being convergent, the Mach lines are divergent, as shown in Figure 15.8(b) and (c). Consequently,
there is a tendency for velocity gradients to decrease with increasing distance from the wall. Thus, an expansion is isentropic throughout the
fluid.
Figure 15.8:
Expansion of supersonic flow via turning. Case (a) shows a single turn through an oblique shock, which is
forbidden on thermodynamic grounds.
Case (b) shows a Prandtl-Mayer expansion fan.
Case (c) shows smooth continuous expansion.
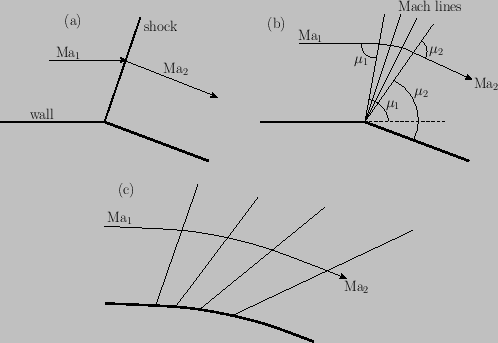 |
The expansion at a corner takes place via a fan of straight Mach lines that is generally known as a
Prandtl-Mayer expansion fan. [See Figure 15.8(b).] The arguments that lead to this conclusion
are as follows.
First, the flow up to the corner is uniform, at Mach number
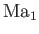 (say), and, thus, the leading Mach line must be straight, and
inclined to the flow at the Mach angle
(say), and, thus, the leading Mach line must be straight, and
inclined to the flow at the Mach angle
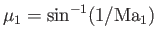 . Because of the limited upstream influence
in supersonic flow, the same argument may be applied to each succeeding portion of the flow. The terminating Mach line stands at the angle
. Because of the limited upstream influence
in supersonic flow, the same argument may be applied to each succeeding portion of the flow. The terminating Mach line stands at the angle
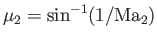 to the wall. Here,
to the wall. Here,
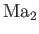 is the Mach number of the downstream flow.
Second, because there is no characteristic length to define a scale in this problem, any variation of flow parameters can only
be with respect to angular position, measured relative to the corner. That is, flow conditions must be constant along
rays emanating from the corner.
is the Mach number of the downstream flow.
Second, because there is no characteristic length to define a scale in this problem, any variation of flow parameters can only
be with respect to angular position, measured relative to the corner. That is, flow conditions must be constant along
rays emanating from the corner.
Figure 15.8(c) shows a typical expansion over a continuous convex turn. Because the
flow is isentropic, it is also reversible (i.e., if the direction of the flow is reversed then the fluid is isentropicaly compressed).
Equation (15.35), which specifies the relationship between  and
and 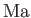 in an isentropic
compression or expansion by turning, can be written
in an isentropic
compression or expansion by turning, can be written
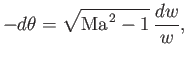 |
(15.36) |
or
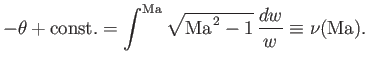 |
(15.37) |
In order to evaluate the integral, and, thus, derive an explicit form for the function
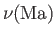 , we need
to rewrite
, we need
to rewrite 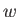 in terms of
in terms of 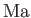 using the definition
using the definition
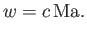 |
(15.38) |
Here, 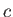 is the local sound speed. Given that
is the local sound speed. Given that
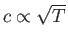 [see Equation (14.45)], it follows from Equation (14.58) that
[see Equation (14.45)], it follows from Equation (14.58) that
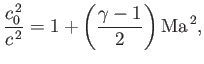 |
(15.39) |
where 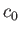 is the stagnation sound speed. Thus,
is the stagnation sound speed. Thus,
![$\displaystyle \frac{dw}{w} = \frac{d{\rm Ma}}{{\rm Ma}}+\frac{dc}{c} = \left(\frac{1}{1+[(\gamma-1)/2]\,{\rm Ma}^{\,2}}\right)\frac{d{\rm Ma}}{{\rm Ma}}.$](img5770.png) |
(15.40) |
The function
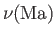 , which is known as the Prandtl-Mayer function, is then given by (see Exercise x)
, which is known as the Prandtl-Mayer function, is then given by (see Exercise x)
Here, the constant of integration has been arbitrarily chosen such that  corresponds to
corresponds to
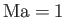 .
A supersonic Mach number,
.
A supersonic Mach number, 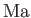 , is thus associated with a definite value of the function
, is thus associated with a definite value of the function 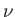 . In fact, as
. In fact, as 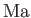 increases from
increases from 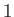 to
to 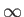 ,
, 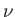 increases monotonically from 0
to
increases monotonically from 0
to
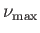 , where
, where
![$\displaystyle \nu_{\rm max} = \frac{\pi}{2}\left[\left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}-1\right].$](img5776.png) |
(15.42) |
Equation (15.37) yields
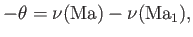 |
(15.43) |
as the relationship between the deflection angle,  , and the Mach number,
, and the Mach number, 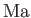 , in an isentropic compression or
expansion by turning.
In a compressive turn,
, in an isentropic compression or
expansion by turning.
In a compressive turn, 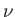 decreases, whereas, in an expansive turn, it increases: in each case, by an amount equal to the
change in
decreases, whereas, in an expansive turn, it increases: in each case, by an amount equal to the
change in  . Here, we have set
. Here, we have set
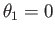 , because only the change in
, because only the change in  matters.
Note that
matters.
Note that  is positive in compressive turns, and negative in expansive turns.
is positive in compressive turns, and negative in expansive turns.
Figure:
Detached shock waves. (a) Detached shock on wedge with afterbody. [At lettered points on the shock, flow
deflection is given by corresponding points in (b).] (b) Deflection angle versus wave angle for
fixed
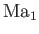 .
.
 |



Next: Detached Shocks
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Compression by Turning
Richard Fitzpatrick
2016-03-31


![]() (say), and, thus, the leading Mach line must be straight, and
inclined to the flow at the Mach angle
(say), and, thus, the leading Mach line must be straight, and
inclined to the flow at the Mach angle
![]() . Because of the limited upstream influence
in supersonic flow, the same argument may be applied to each succeeding portion of the flow. The terminating Mach line stands at the angle
. Because of the limited upstream influence
in supersonic flow, the same argument may be applied to each succeeding portion of the flow. The terminating Mach line stands at the angle
![]() to the wall. Here,
to the wall. Here,
![]() is the Mach number of the downstream flow.
Second, because there is no characteristic length to define a scale in this problem, any variation of flow parameters can only
be with respect to angular position, measured relative to the corner. That is, flow conditions must be constant along
rays emanating from the corner.
is the Mach number of the downstream flow.
Second, because there is no characteristic length to define a scale in this problem, any variation of flow parameters can only
be with respect to angular position, measured relative to the corner. That is, flow conditions must be constant along
rays emanating from the corner.
![]() and
and ![]() in an isentropic
compression or expansion by turning, can be written
in an isentropic
compression or expansion by turning, can be written
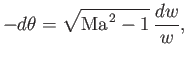
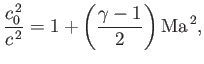
![$\displaystyle \frac{dw}{w} = \frac{d{\rm Ma}}{{\rm Ma}}+\frac{dc}{c} = \left(\frac{1}{1+[(\gamma-1)/2]\,{\rm Ma}^{\,2}}\right)\frac{d{\rm Ma}}{{\rm Ma}}.$](img5770.png)
![$\displaystyle \equiv \int_1^{{\rm Ma}}\frac{\sqrt{M^{\,2}-1}}{1+[(\gamma-1)/2]\,M^{\,2}}\,\frac{dM}{M}$](img5772.png)
![$\displaystyle = \left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}\tan^{-1}\left(\lef...
...\right]^{1/2}\right)-\tan^{-1}\left(\left[{\rm Ma}^{\,2}-1\right]^{1/2}\right).$](img5773.png)
![$\displaystyle \nu_{\rm max} = \frac{\pi}{2}\left[\left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}-1\right].$](img5776.png)
