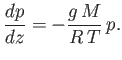Next: Adiabatic Atmosphere
Up: Equilibrium of Compressible Fluids
Previous: Introduction
The vertical thickness of the atmosphere is only a few tens of kilometers, and is, therefore, much less than the
radius of the Earth, which is about
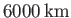 . Consequently, it is a good approximation to treat the atmosphere
as a relatively thin layer, covering the surface of the Earth, in which the pressure and density are only functions of altitude above ground level,
. Consequently, it is a good approximation to treat the atmosphere
as a relatively thin layer, covering the surface of the Earth, in which the pressure and density are only functions of altitude above ground level,  , and the
gravitational potential energy per unit mass takes the form
, and the
gravitational potential energy per unit mass takes the form
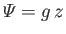 , where
, where 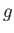 is the acceleration due to
gravity at
is the acceleration due to
gravity at  . It follows from Equation (13.1) that
. It follows from Equation (13.1) that
 |
(13.5) |
Now, in an isothermal atmosphere, in which the temperature, 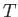 , is assumed not to vary with height,
the ideal gas equation of state (1.84) yields [cf., Equation (13.3)]
, is assumed not to vary with height,
the ideal gas equation of state (1.84) yields [cf., Equation (13.3)]
 |
(13.6) |
The previous two equations can be combined to give
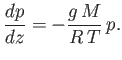 |
(13.7) |
Hence, we obtain
 |
(13.8) |
where
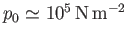 is atmospheric pressure at ground level, and
is atmospheric pressure at ground level, and
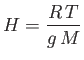 |
(13.9) |
is known as the isothermal scale height of the atmosphere. Using the values
 (
(
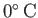 ),
),
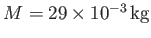 ,
and
,
and
 , which are typical of the Earth's atmosphere (at ground level), as well as
, which are typical of the Earth's atmosphere (at ground level), as well as
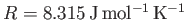 , we find that
, we find that
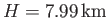 .
Equations (13.6) and (13.8) yield
.
Equations (13.6) and (13.8) yield
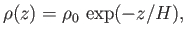 |
(13.10) |
where
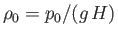 is the atmospheric mass density at
is the atmospheric mass density at  . According to Equations (13.8) and
(13.10), in an isothermal atmosphere, the pressure and density both decrease exponentially with increasing altitude, falling
to
. According to Equations (13.8) and
(13.10), in an isothermal atmosphere, the pressure and density both decrease exponentially with increasing altitude, falling
to 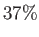 of their values at ground level when
of their values at ground level when 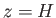 , and to only
, and to only  of these values when
of these values when  .
.



Next: Adiabatic Atmosphere
Up: Equilibrium of Compressible Fluids
Previous: Introduction
Richard Fitzpatrick
2016-03-31