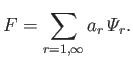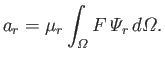

Next: Auxilliary Eigenfunctions
Up: Terrestrial Ocean Tides
Previous: Another Useful Lemma
Basis Eigenfunctions
Suppose that the
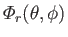 are well-behaved solutions of the eigenvalue equation
are well-behaved solutions of the eigenvalue equation
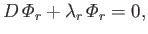 |
(12.230) |
subject to the boundary conditions
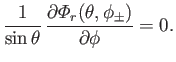 |
(12.231) |
It immediately follows from Equations (12.234) and (12.235) that
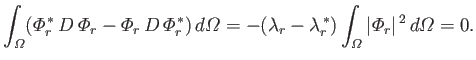 |
(12.232) |
Hence, we deduce that the 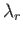 are real. It follows that we can choose the
are real. It follows that we can choose the
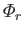 to be real functions. Equations (12.234) and (12.235) also
yield
to be real functions. Equations (12.234) and (12.235) also
yield
![$\displaystyle \int_{\mit\Omega} {\mit\Phi}_r\,D\,{\mit\Phi}_r\,d{\mit\Omega} = ...
...heta}\,\frac{\partial {\mit\Phi}_r}{\partial\phi}\right)^2\right]d{\mit\Omega},$](img4810.png) |
(12.233) |
which implies that the 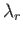 are positive. Integration of Equation (12.235), subject to the boundary condition (12.236), gives
are positive. Integration of Equation (12.235), subject to the boundary condition (12.236), gives
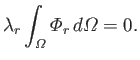 |
(12.234) |
Because 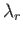 is positive, this implies that
is positive, this implies that
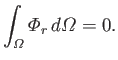 |
(12.235) |
Finally, Equations (12.234) and (12.235) yield
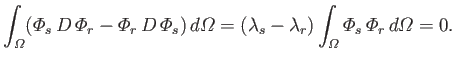 |
(12.236) |
It follows that
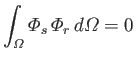 |
(12.237) |
if
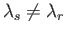 . As is well known (Riley 1974), if
. As is well known (Riley 1974), if
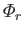 and
and
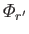 are linearly independent solutions of (12.235) corresponding to the same
eigenvalue,
are linearly independent solutions of (12.235) corresponding to the same
eigenvalue, 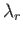 , then it is always possible to choose linear combinations of them that satisfy
, then it is always possible to choose linear combinations of them that satisfy
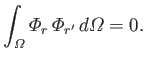 |
(12.238) |
This argument can be extended to multiple linearly independent solutions corresponding to the same eigenvalue. Hence, we conclude that it
is possible to choose the
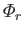 such that they satisfy the orthonormality condition
such that they satisfy the orthonormality condition
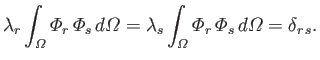 |
(12.239) |
Let
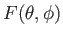 be a well-behaved function. Suppose that
be a well-behaved function. Suppose that
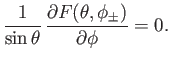 |
(12.240) |
We can automatically satisfy the previous boundary condition by writing
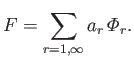 |
(12.241) |
(Note that 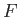 is undetermined to an arbitrary additive constant which is chosen so as to ensure that
is undetermined to an arbitrary additive constant which is chosen so as to ensure that
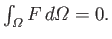 )
Here,
)
Here, 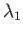 is the smallest eigenvalue of Equation (12.235),
is the smallest eigenvalue of Equation (12.235), 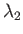 the next smallest eigenvalue, and so on.
It follows from Equation (12.244) that
the next smallest eigenvalue, and so on.
It follows from Equation (12.244) that
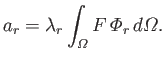 |
(12.242) |
Suppose that the
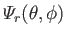 are well-behaved solutions of the eigenvalue equation
are well-behaved solutions of the eigenvalue equation
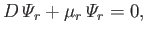 |
(12.243) |
subject to the boundary conditions
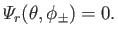 |
(12.244) |
Using analogous arguments to those employed previously, we can show that the 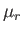 are real
and positive, and that the
are real
and positive, and that the
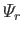 can be chosen so as to satisfy the orthonormality constraint
can be chosen so as to satisfy the orthonormality constraint
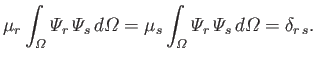 |
(12.245) |
Let
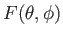 be a well-behaved function. Suppose that
be a well-behaved function. Suppose that
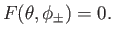 |
(12.246) |
We can automatically satisfy the previous boundary condition by writing
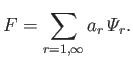 |
(12.247) |
It follows from Equation (12.250) that
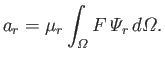 |
(12.248) |


Next: Auxilliary Eigenfunctions
Up: Terrestrial Ocean Tides
Previous: Another Useful Lemma
Richard Fitzpatrick
2016-03-31
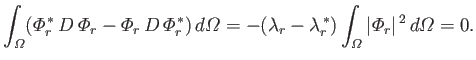
![$\displaystyle \int_{\mit\Omega} {\mit\Phi}_r\,D\,{\mit\Phi}_r\,d{\mit\Omega} = ...
...heta}\,\frac{\partial {\mit\Phi}_r}{\partial\phi}\right)^2\right]d{\mit\Omega},$](img4810.png)
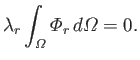
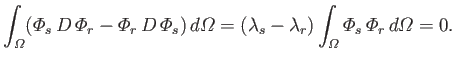
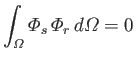
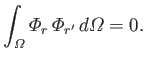
![]() be a well-behaved function. Suppose that
be a well-behaved function. Suppose that
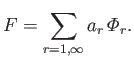
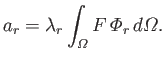
![]() are well-behaved solutions of the eigenvalue equation
are well-behaved solutions of the eigenvalue equation
![]() be a well-behaved function. Suppose that
be a well-behaved function. Suppose that