


Next: Total Gravitational Potential
Up: Terrestrial Ocean Tides
Previous: Surface Harmonics and Solid
Planetary Rotation
Suppose that the planet is rotating rigidly about the axis 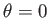 at the angular velocity
at the angular velocity
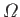 (where
(where
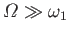 ).
The planet's rotational angular velocity vector is thus
).
The planet's rotational angular velocity vector is thus
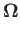  |
(12.43) |
Let
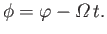 |
(12.44) |
It follows that 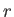 ,
, 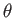 ,
, 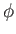 are spherical coordinates in a frame of reference that co-rotates with the planet.
are spherical coordinates in a frame of reference that co-rotates with the planet.
Richard Fitzpatrick
2016-03-31