


Next: Expansion of Tide Generating
Up: Terrestrial Ocean Tides
Previous: Tide Generating Potential
Decomposition of Tide Generating Potential
Let  ,
,  ,
, 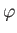 be right-handed spherical coordinates in a non-rotating reference frame whose origin lies at the center of the planet,
and whose symmetry axis coincides with the planetary rotation axis. Thus, the vector position of a
general point is
be right-handed spherical coordinates in a non-rotating reference frame whose origin lies at the center of the planet,
and whose symmetry axis coincides with the planetary rotation axis. Thus, the vector position of a
general point is
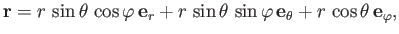 |
(12.15) |
where
 , et cetera.
Let the coordinates of the moon's center be
, et cetera.
Let the coordinates of the moon's center be  ,
,  ,
,  . It follows that
. It follows that
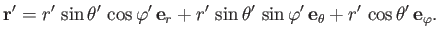 |
(12.16) |
Hence, from Equation (12.5),
 |
(12.17) |
Now, according to the spherical harmonic addition theorem (Arfken 1985),
which implies that
Here,
![$\displaystyle P_n^{\,m}(x)=(-1)^m\,(1-x^{\,2})^{m/2}\,\frac{d^{\,m}[P_n(x)]}{dx^{\,m}},$](img4263.png) |
(12.21) |
for 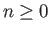 and
and 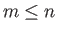 , denotes an associated Legendre function (Abramowitz and Stegun 1965). In particular,
, denotes an associated Legendre function (Abramowitz and Stegun 1965). In particular,
Note that
 .
.
Let
where 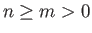 . According to Equations (12.14), (12.20), and (12.25)-(12.27),
. According to Equations (12.14), (12.20), and (12.25)-(12.27),
Here, we have neglected the unimportant constant term in Equation (12.14).



Next: Expansion of Tide Generating
Up: Terrestrial Ocean Tides
Previous: Tide Generating Potential
Richard Fitzpatrick
2016-03-31
![$\displaystyle \phantom{=} + 2\sum_{m=1,n}\frac{(n-m)!}{(n+m)!}\,P_n^{\,m}(\cos\theta)\,P_n^{\,m}(\cos\theta')\,\cos[m\,(\varphi-\varphi')],$](img4259.png)
![$\displaystyle P_n^{\,m}(x)=(-1)^m\,(1-x^{\,2})^{m/2}\,\frac{d^{\,m}[P_n(x)]}{dx^{\,m}},$](img4263.png)