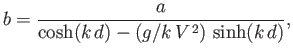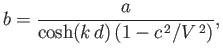Next: Surface Tension
Up: Waves in Incompressible Fluids
Previous: Gravity Waves at an
Steady Flow over a Corrugated Bottom
Consider a stream of water of mean depth  , and uniform horizontal velocity
, and uniform horizontal velocity
 , that flows over a corrugated bottom
whose elevation is
, that flows over a corrugated bottom
whose elevation is
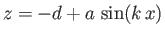 , where
, where  is much smaller than
is much smaller than  . Let the elevation of the free surface of the water
be
. Let the elevation of the free surface of the water
be
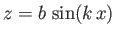 . We wish to determine the relationship between
. We wish to determine the relationship between  and
and 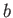 .
.
We expect the velocity potential, perturbed pressure, and vertical displacement of the water to be of the form (11.91), (11.92), and
(11.93), respectively,
with
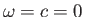 , because we are looking for a stationary (i.e., non-propagating) perturbation driven by the static
corrugations in the bottom. The boundary condition at the bottom is
, because we are looking for a stationary (i.e., non-propagating) perturbation driven by the static
corrugations in the bottom. The boundary condition at the bottom is
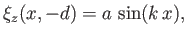 |
(11.104) |
which yields
![$\displaystyle V^{\,-1}\left[-A\,\sinh(k\,d)+ B\,\cosh(k\,d)\right] = a.$](img4122.png) |
(11.105) |
At the free surface, we have
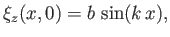 |
(11.106) |
which gives
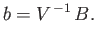 |
(11.107) |
In addition, pressure balance across the free surface yields
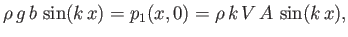 |
(11.108) |
which leads to
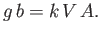 |
(11.109) |
Hence, from Equations (11.105), (11.107), and (11.109),
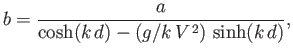 |
(11.110) |
or
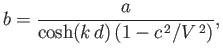 |
(11.111) |
where
![$ c=[(g/k)\,\tanh(k\,d)]^{1/2}$](img4129.png) is the phase velocity of a gravity wave of wave number
is the phase velocity of a gravity wave of wave number 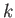 .
[See Equation (11.21).]
It follows that the peaks and troughs of the free surface coincide with those of the bottom when
.
[See Equation (11.21).]
It follows that the peaks and troughs of the free surface coincide with those of the bottom when 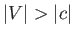 , and
the troughs coincide with the peaks, and vice versa, when
, and
the troughs coincide with the peaks, and vice versa, when 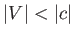 . If
. If 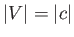 then the ratio
then the ratio 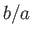 becomes infinite, implying that the
oscillations driven by the corrugations are not of small amplitude, and, therefore, cannot be described by linear theory.
becomes infinite, implying that the
oscillations driven by the corrugations are not of small amplitude, and, therefore, cannot be described by linear theory.



Next: Surface Tension
Up: Waves in Incompressible Fluids
Previous: Gravity Waves at an
Richard Fitzpatrick
2016-03-31
![]() , because we are looking for a stationary (i.e., non-propagating) perturbation driven by the static
corrugations in the bottom. The boundary condition at the bottom is
, because we are looking for a stationary (i.e., non-propagating) perturbation driven by the static
corrugations in the bottom. The boundary condition at the bottom is