


Next: Flow Between Parallel Plates
Up: Incompressible Viscous Flow
Previous: Incompressible Viscous Flow
Introduction
This chapter investigates incompressible flow in which viscosity plays a significant role throughout the bulk of the fluid. Such flow generally
takes place at relatively low Reynolds number. From Section 1.14, the equations governing incompressible viscous fluid motion can be written
where the quantity
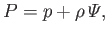 |
(10.3) |
which is a combination of the actual fluid pressure,  , and the gravitational potential energy per unit volume,
, and the gravitational potential energy per unit volume,
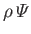 , is
known as the effective pressure. Here,
, is
known as the effective pressure. Here,  is the fluid mass density,
is the fluid mass density, 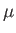 the fluid viscosity, and
the fluid viscosity, and
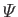 the gravitational potential. More information on this topic can be found in Batchelor 2000.
the gravitational potential. More information on this topic can be found in Batchelor 2000.
Richard Fitzpatrick
2016-03-31