Three-Dimensional Airfoils

Let us now take into account the fact that realistic three-dimensional airfoils are of finite size. Consider Figure 9.8, which shows a top view of a stationary airfoil of finite size, situated in a (predominately) horizontal wind of velocity ${\bf V}= V\,{\bf e}_\parallel$ . In the following, we shall sometimes refer to such an airfoil as a wing (although it actually represents a pair of wings on a standard fixed wing aircraft). Let us adopt the coordinate system shown in the figure, which is such that the $x$ -$z$ plane is horizontal, the wind is incident predominately from the $x$ -direction, and the $y$ -axis points vertically upward. The wing is assumed to lie in the $x$ -$z$ plane. Let $b$ be the wingspan, and let $c(z)$ and $\delta(z)$ be the width and thickness, respectively, of the wing cross-section (parallel to the $x$ -$y$ plane). (See Figure 9.9.) Suppose that the wing is symmetric about the median plane, $z=0$ , so that $c(-z)=c(z)$ and $\delta(-z)=\delta(z)$ . It follows that $c(z>b/2)=\delta(z>b/2)=0$ : that is, the wing extends from $z=-b/2$ to $z=b/2$ .

Figure 9.8: Top view of a three-dimensional airfoil of finite size.

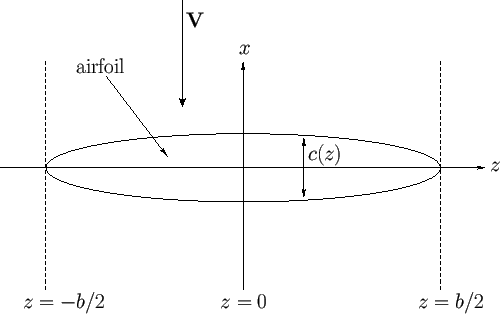
Suppose that air circulation is set up around the wing parallel to the $x$ -$y$ plane in such a manner as to produce an upward lift. It follows that the average pressure on the lower surface of the wing must exceed that on its upper surface. Consider Figure 9.9, which shows a back view of the airfoil shown in Figure 9.8. As we go from the median plane ($z=0$ ) to a wing tip, $Y$ , whether along the upper or the lower surface of the wing, we must arrive at the same pressure at $Y$ . It follows that there is a drop in pressure as we move outward, away from the median plane, along the wing's bottom surface, and a further drop in pressure as we move inward, toward the median plane, along the upper surface. Because air is pushed in the direction of decreasing pressure, it follows that the air that impinges on the wing's leading edge, and then passes over its upper surface, deviates sideways toward the median plane. Likewise, the air that passes over the wing's lower surface deviates sideways away from the median plane. (See Figure 9.8.)

Figure 9.9: Back view of a three-dimensional airfoil of finite size, indication the pressure variation over its surface.

The air that leaves the trailing edge of the wing at some point $Q$ must have impinged on the leading edge at the different points $P$ and $P'$ , depending on whether it travelled over the wing's upper or lower surfaces, respectively. Moreover, air that travels to $Q$ via the wing's upper surface acquires a small sideways velocity directed towards the median plane, whereas that which travels to $Q$ via the lower surface acquires a small sideways velocity directed away from the median plane. On the other hand, the air speed at $Q$ must be the same, irrespective of whether the air arrives from the wing's upper or lower surface, because the pressure (which, according to Bernoulli's theorem, depends on the air speed) must be continuous at $Q$ . Thus, we conclude that there is a discontinuity in the direction of the air emitted by the trailing edge of a wing. This implies that the interface, ${\mit\Sigma}$ , between the two streams of air that travel over the upper and lower surfaces of the wing is a vortex sheet. (See Section 9.5.) Of course, this vortex sheet constitutes the wake that trails behind the airfoil. Moreover, we would generally expect the wake to be convected by the incident wind. It follows that the vorticity per unit length in the wake can be written

$$\mbox{\boldmath$\Omega$} _{\mit\Sigma}= -I(z)\,{\bf e}_\parallel,$$ (9.63)

where $I(z)=-{\mit\Delta} v_z$ , and ${\mit\Delta} v_z$ is tangential velocity discontinuity across the wake. [See Equation (9.56).]

Figure 9.10: Top view of the airflow over the top (left) and bottom (right) surfaces of a three-dimensional airfoil of finite size.

As we saw previously, the boundary layer that covers the airfoil is such that the tangential velocity ${\bf U}$ just outside the layer is sharply reduced to zero at the airfoil surface. Actually, the nature of the substance enclosed by the surface is irrelevant to our argument, and nothing is changed in our analysis if we suppose that this region contains air at rest. Thus, we can replace the airfoil by air at rest, and the boundary layer by a vortex sheet, $S$ , with a vortex intensity per unit length $\Omega$ $_S$ that is determined by the velocity discontinuity ${\bf U}$ between the air just outside the boundary layer and that at rest in the region where the airfoil was previously located. In fact, Equation (9.56) yields

$$\mbox{\boldmath$\Omega$} _S = {\bf n}\times {\bf U},$$ (9.64)

where ${\bf n}$ is an outward unit normal to the airfoil surface.

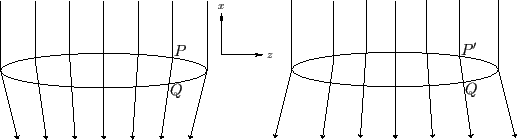
We conclude that a stationary airfoil situated in a uniform wind of constant velocity is equivalent to a vortex sheet $S$ , located at the airfoil surface, and a wake ${\mit\Sigma}$ that trails behind the airfoil, the airfoil itself being replaced by air at rest. The vorticity within $S$ is largely parallel to the $z$ -axis [because ${\bf n}$ and ${\bf U}$ are both essentially parallel to the $x$ -$y$ plane--see Equation (9.64)], whereas that in ${\mit\Sigma}$ is parallel to the incident wind direction. (See Figure 9.11.) The vortex filaments within $S$ are generally termed bound filaments (because they cannot move off the airfoil surface). Conversely, the vortex filaments within ${\mit\Sigma}$ are generally termed free filaments. The air velocity both inside and outside $S$ can be written

$${\bf v} = {\bf V} + {\bf v}_{\mit\Sigma}+ {\bf v}_S,$$ (9.65)

where ${\bf V}$ is the external wind velocity, ${\bf v}_{\mit\Sigma}$ the velocity field induced by the free vortex filaments that constitute ${\mit\Sigma}$ , and ${\bf v}_S$ the velocity field induced by the bound filaments that constitute $S$ .

Figure 9.11: Vortex structure around a wing.

Consider some point $P$ that lies on $S$ . Let $P_+$ and $P_-$ be two neighboring points that are equidistant from $P$ , where $P_+$ lies just outside $S$ , and $P_-$ lies just inside $S$ , and the line $P_-P_+$ is normal to $S$ . We can write

$${\bf v}(P_+) = {\bf V} + {\bf v}_{\mit\Sigma}(P_+)+ {\bf v}_S(P_+),$$ (9.66)

$${\bf v}(P_-) = {\bf V} + {\bf v}_{\mit\Sigma}(P_-)+ {\bf v}_S(P_-).$$ (9.67)

However, ${\bf v}(P_+) = {\bf U}(P)$ , where ${\bf U}(P)$ is the tangential air velocity just above point $P$ on the airfoil surface, and ${\bf v}(P_-)={\bf0}$ , as the air within $S$ is stationary. Moreover, ${\bf v}_{\mit\Sigma}(P_+)={\bf v}_{\mit\Sigma}(P_-)= {\bf v}_{\mit\Sigma}(P)$ , because we expect ${\bf v}_{\mit\Sigma}$ to be continuous across $S$ . On the other hand, we expect the tangential component of ${\bf v}_S$ to be discontinuous across $S$ . Let us define

$${\bf v}_S(P)= \frac{1}{2}\left[{\bf v}_S(P_+)+ {\bf v}_S(P_-)\right].$$ (9.68)

This quantity can be identified as the velocity induced at point $P$ by the bound vortices on $S$ , excluding the contribution from the local bound vortex at $P$ (because this vortex induces equal and opposite velocities at $P_+$ and $P_-$ ). Finally, taking half the sum of Equations (9.66) and (9.67), we obtain

$$\frac{1}{2}\,{\bf U}(P) = {\bf V} + {\bf v}_{\mit\Sigma}(P)+ {\bf v}_S(P).$$ (9.69)