


Next: Flow Around a Submerged
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Conformal Maps
Consider the conformal map
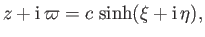 |
(7.115) |
where 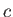 is real and positive. It follows that
is real and positive. It follows that
Let
Thus, in the meridian plane, the curve 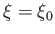 corresponds to the ellipse
corresponds to the ellipse
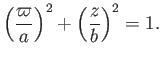 |
(7.120) |
We conclude that the surface 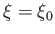 is an oblate spheroid (i.e., the three-dimensional surface obtained by
rotating an ellipse about a minor axis) of major radius
is an oblate spheroid (i.e., the three-dimensional surface obtained by
rotating an ellipse about a minor axis) of major radius  and minor radius
and minor radius 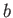 .
The constraints (7.87) and (7.90) yield
.
The constraints (7.87) and (7.90) yield
respectively. Setting
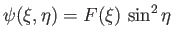 , and substituting into the governing equation, (7.86), we obtain
, and substituting into the governing equation, (7.86), we obtain
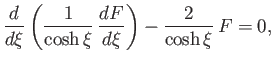 |
(7.123) |
which can be rearranged to give
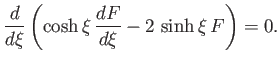 |
(7.124) |
On integration, we get
 |
(7.125) |
which can be rearranged to give
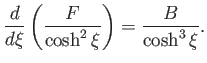 |
(7.126) |
It follows that
where use has been made of the constraint (7.121).
Let
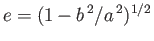 be the eccentricity of the spheroid. Thus,
be the eccentricity of the spheroid. Thus,
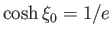 ,
,
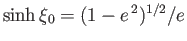 ,
,
 , and
, and
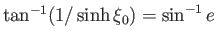 . The constraint (7.122) yields
. The constraint (7.122) yields
![$\displaystyle -\frac{1}{2}\,V\,a^{\,2} = F(\xi_0)= \frac{1}{2}\,B\left[\frac{(1-e^{\,2})^{1/2}}{e}-\frac{\sin^{-1}e}{e^{\,2}}\right],$](img2773.png) |
(7.128) |
or
![$\displaystyle B = - \left[\frac{V\,a^{\,2}\,e^{\,2}}{e\,(1-e^{\,2})^{1/2}-\sin^{-1}e}\right].$](img2774.png) |
(7.129) |
Hence,
![$\displaystyle \psi(\xi,\eta) =-\frac{1}{2}\,V\,a^{\,2}\,e^{\,2}\left[\frac{\sin...
...\xi\,\tan^{-1}(1/\sinh\xi)} {e\,(1-e^{\,2})^{1/2}-\sin^{-1}e}\right]\sin^2\eta.$](img2775.png) |
(7.130) |
Finally, from Equation (7.84),
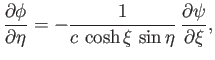 |
(7.131) |
which can be integrated to give
![$\displaystyle \phi(\xi,\eta) =-V\,a\,e\left[\frac{1 -\sinh\xi\,\tan^{-1}(1/\sinh\xi)} {e\,(1-e^{\,2})^{1/2}-\sin^{-1}e}\right]\cos\eta.$](img2777.png) |
(7.132) |
It is easily demonstrated that
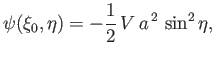 |
(7.133) |
and
![$\displaystyle \phi(\xi_0,\eta) = V\,a\left[\frac{e-(1-e^{\,2})^{1/2}\,\sin^{-1} e}{\sin^{-1} e-e\,(1-e^{\,2})^{1/2}}\right]\cos\eta.$](img2779.png) |
(7.134) |
Thus,
![$\displaystyle K = -\pi\,\rho\left.\int_{\eta=0}^{\eta=\pi} \phi\,d\psi\right\ve...
...rac{e-(1-e^{\,2})^{1/2}\,\sin^{-1} e}{\sin^{-1} e-e\,(1-e^{\,2})^{1/2}}\right].$](img2780.png) |
(7.135) |
It follows that the added mass of the spheroid is
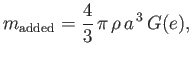 |
(7.136) |
where
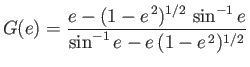 |
(7.137) |
is a monotonic function that varies between 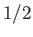 when
when  and
and 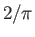 when
when  .
.
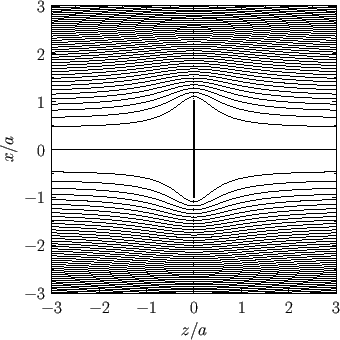
Figure:
Contours of the Stokes stream function for the case of a disk of radius  , lying in the
, lying in the  -
- plane, and placed in a uniform, incompressible, irrotational flow directed parallel to the
plane, and placed in a uniform, incompressible, irrotational flow directed parallel to the  -axis.
-axis.
 |
In the limit
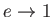 , our spheroid asymptotes to a thin disk of radius
, our spheroid asymptotes to a thin disk of radius  moving through the fluid in the direction
perpendicular to its plane. Expressions (7.130), (7.132), and (7.136) yield
moving through the fluid in the direction
perpendicular to its plane. Expressions (7.130), (7.132), and (7.136) yield
and
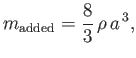 |
(7.140) |
respectively. Here,
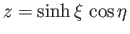 and
and
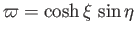 . It
follows that, in the instantaneous rest frame of the disk,
. It
follows that, in the instantaneous rest frame of the disk,
![$\displaystyle \psi(\varpi,z)=- \frac{1}{4}\,V\left[a^{\,2}+z^{\,2}+\varpi^{\,2}...
...rpi^{\,2})^2-4\,a^{\,2}\,\varpi^{\,2}}\,\right] + \frac{1}{2}\,V\,\varpi^{\,2}.$](img2794.png) |
(7.141) |
This flow pattern, which corresponds to that of a thin disk placed in a uniform flow perpendicular to its plane, is visualized in Figure 7.6.



Next: Flow Around a Submerged
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Conformal Maps
Richard Fitzpatrick
2016-03-31
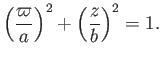
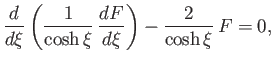
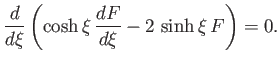

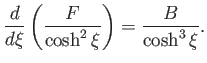
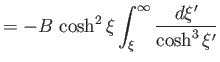
![$\displaystyle =-\frac{1}{2}\, B\,\cosh^2\xi\left[ \frac{\sinh\xi'}{\cosh^2\xi'}-\tan^{-1}\left(\frac{1}{\sinh\xi'}\right)\right]^{\infty}_{\xi}$](img2766.png)
![$\displaystyle = \frac{1}{2}\,B\left[\sinh\xi -\cosh^2\xi\,\tan^{-1}\left(\frac{1}{\sinh\xi}\right)\right],$](img2767.png)
![$\displaystyle -\frac{1}{2}\,V\,a^{\,2} = F(\xi_0)= \frac{1}{2}\,B\left[\frac{(1-e^{\,2})^{1/2}}{e}-\frac{\sin^{-1}e}{e^{\,2}}\right],$](img2773.png)
![$\displaystyle B = - \left[\frac{V\,a^{\,2}\,e^{\,2}}{e\,(1-e^{\,2})^{1/2}-\sin^{-1}e}\right].$](img2774.png)
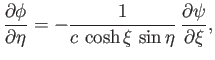
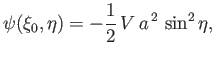
![$\displaystyle \phi(\xi_0,\eta) = V\,a\left[\frac{e-(1-e^{\,2})^{1/2}\,\sin^{-1} e}{\sin^{-1} e-e\,(1-e^{\,2})^{1/2}}\right]\cos\eta.$](img2779.png)
![$\displaystyle K = -\pi\,\rho\left.\int_{\eta=0}^{\eta=\pi} \phi\,d\psi\right\ve...
...rac{e-(1-e^{\,2})^{1/2}\,\sin^{-1} e}{\sin^{-1} e-e\,(1-e^{\,2})^{1/2}}\right].$](img2780.png)
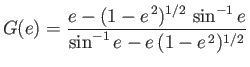

![]() , our spheroid asymptotes to a thin disk of radius
, our spheroid asymptotes to a thin disk of radius ![]() moving through the fluid in the direction
perpendicular to its plane. Expressions (7.130), (7.132), and (7.136) yield
moving through the fluid in the direction
perpendicular to its plane. Expressions (7.130), (7.132), and (7.136) yield
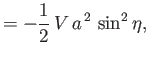
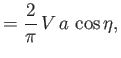
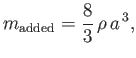
![$\displaystyle \psi(\varpi,z)=- \frac{1}{4}\,V\left[a^{\,2}+z^{\,2}+\varpi^{\,2}...
...rpi^{\,2})^2-4\,a^{\,2}\,\varpi^{\,2}}\,\right] + \frac{1}{2}\,V\,\varpi^{\,2}.$](img2794.png)