


Next: Flow Past a Spherical
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Point Sources
Consider the flow pattern generated by point source of strength  located on the symmetry axis at
located on the symmetry axis at 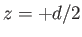 , and
a point source of strength
, and
a point source of strength  (i.e., a point sink) located on the symmetry axis at
(i.e., a point sink) located on the symmetry axis at 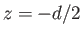 .
It follows, by analogy with the analysis of the previous section, that the stream function and velocity potential at a general
point,
.
It follows, by analogy with the analysis of the previous section, that the stream function and velocity potential at a general
point,  , lying in the meridian plane, are
, lying in the meridian plane, are
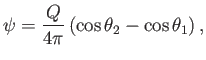 |
(7.36) |
and
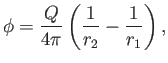 |
(7.37) |
respectively. Here, 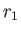 ,
,  ,
, 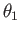 , and
, and 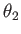 are defined in Figure 7.2.
are defined in Figure 7.2.
Figure 7.2:
A dipole source.
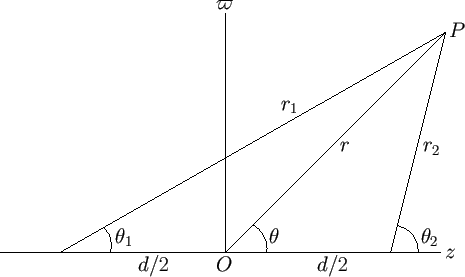 |
In the limit that the product 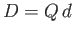 remains constant, while
remains constant, while
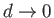 , we obtain a so-called dipole point source.
According to the sine rule of trigonometry,
, we obtain a so-called dipole point source.
According to the sine rule of trigonometry,
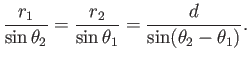 |
(7.38) |
However,
![$ \sin(\theta_2-\theta_1)= 2\,\sin[(\theta_2-\theta_1)/2]\,\cos[(\theta_2-\theta_1)/2]$](img2623.png) , so
we obtain
, so
we obtain
![$\displaystyle r_1-r_2 = \frac{d\,(\sin\theta_2-\sin\theta_1)}{2\,\sin[(\theta_2-\theta_1)/2]\,\cos[(\theta_2-\theta_1)/2]}.$](img2624.png) |
(7.39) |
In fact,
![$ \sin\theta_2-\sin\theta_1 = 2\,\cos[(\theta_2+\theta_1)/2]\,\sin[(\theta_2-\theta_1)/2]$](img2625.png) ,
which leads to
,
which leads to
![$\displaystyle r_1 - r_2= \frac{d\,\cos[(\theta_2+\theta_1)/2]}{\cos[(\theta_2-\theta_1)/2]}.$](img2626.png) |
(7.40) |
Thus, in the limit
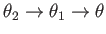 and
and
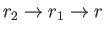 ,
we get
,
we get
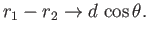 |
(7.41) |
Hence, according to Equation (7.37),
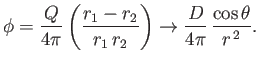 |
(7.42) |
Equation (7.36) implies that
![$\displaystyle \psi = \frac{Q}{4\pi}\left(\frac{z-d/2}{r_2}-\frac{z+d/2}{r_1}\ri...
...frac{1}{r_1}\right)-\frac{d}{2}\left(\frac{1}{r_2}+\frac{1}{r_1}\right)\right].$](img2631.png) |
(7.43) |
Thus, in the limit
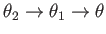 and
and
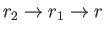 ,
we obtain
,
we obtain
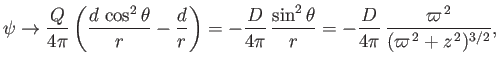 |
(7.44) |
where use has been made of Equation (7.41), as well as the fact that
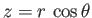 .
Figure 7.3 shows the stream function of a dipole point source located at the origin.
.
Figure 7.3 shows the stream function of a dipole point source located at the origin.
Figure 7.3:
Contours of the stream function of a dipole source located at the origin.
 |
Incidentally, Equations (7.26), (7.28), (7.33), (7.35), (7.42), and (7.44) imply that the terms in the
expansions (7.23) and (7.24) involving the constants 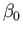 ,
, 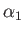 , and
, and  correspond to
a point source at the origin, uniform flow parallel to the
correspond to
a point source at the origin, uniform flow parallel to the  -axis, and a dipole point source at the origin, respectively.
Of course, the term involving
-axis, and a dipole point source at the origin, respectively.
Of course, the term involving  is constant, and, therefore, gives rise to no flow.
is constant, and, therefore, gives rise to no flow.



Next: Flow Past a Spherical
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Point Sources
Richard Fitzpatrick
2016-03-31
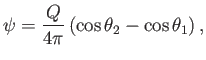
![]() remains constant, while
remains constant, while
![]() , we obtain a so-called dipole point source.
According to the sine rule of trigonometry,
, we obtain a so-called dipole point source.
According to the sine rule of trigonometry,
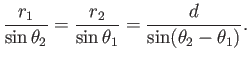
![$\displaystyle r_1-r_2 = \frac{d\,(\sin\theta_2-\sin\theta_1)}{2\,\sin[(\theta_2-\theta_1)/2]\,\cos[(\theta_2-\theta_1)/2]}.$](img2624.png)
![$\displaystyle r_1 - r_2= \frac{d\,\cos[(\theta_2+\theta_1)/2]}{\cos[(\theta_2-\theta_1)/2]}.$](img2626.png)
![$\displaystyle \psi = \frac{Q}{4\pi}\left(\frac{z-d/2}{r_2}-\frac{z+d/2}{r_1}\ri...
...frac{1}{r_1}\right)-\frac{d}{2}\left(\frac{1}{r_2}+\frac{1}{r_1}\right)\right].$](img2631.png)
![]() ,
, ![]() , and
, and ![]() correspond to
a point source at the origin, uniform flow parallel to the
correspond to
a point source at the origin, uniform flow parallel to the ![]() -axis, and a dipole point source at the origin, respectively.
Of course, the term involving
-axis, and a dipole point source at the origin, respectively.
Of course, the term involving ![]() is constant, and, therefore, gives rise to no flow.
is constant, and, therefore, gives rise to no flow.