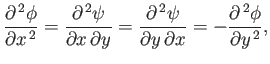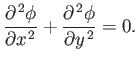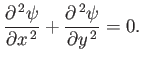Next: Two-Dimensional Uniform Flow
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Flow
As we have seen, a two-dimensional velocity field in which the flow is everywhere parallel to the  -
- plane, and there is
no variation along the
plane, and there is
no variation along the 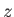 -direction, takes the form
-direction, takes the form
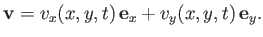 |
(5.16) |
Moreover, if the flow is irrotational then
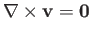 is automatically satisfied by writing
is automatically satisfied by writing
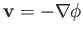 , where
, where
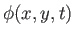 is termed the velocity potential. (See Section 4.15.) Hence,
is termed the velocity potential. (See Section 4.15.) Hence,
On the other hand, if the flow is incompressible then
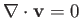 is automatically
satisfied by writing
is automatically
satisfied by writing
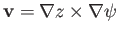 , where
, where
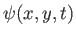 is termed the
stream function. (See Section 5.2.) Hence,
is termed the
stream function. (See Section 5.2.) Hence,
Finally, if the flow is both irrotational and incompressible then Equations (5.17)-(5.18) and
(5.19)-(5.20) hold simultaneously, which implies that
It immediately follows, from the previous two expressions, that
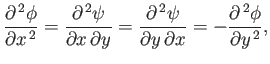 |
(5.23) |
or
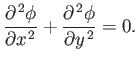 |
(5.24) |
Likewise, it can also be shown that
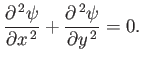 |
(5.25) |
We conclude that, for two-dimensional, irrotational, incompressible flow, the velocity potential and the stream function
both satisfy Laplace's equation.
Equations (5.21) and (5.22) also imply that
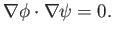 |
(5.26) |
In other words, the contours of the velocity potential and the stream function cross at right-angles.



Next: Two-Dimensional Uniform Flow
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Flow
Richard Fitzpatrick
2016-01-22