


Next: Axisymmetric Soap-Bubbles
Up: Surface Tension
Previous: Jurin's Law
Let adopt Cartesian coordinates on the Earth's surface such that  increases vertically upward. Suppose
that the interface of a liquid of density
increases vertically upward. Suppose
that the interface of a liquid of density  and surface tension
and surface tension 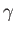 with the atmosphere corresponds to the
surface
with the atmosphere corresponds to the
surface 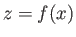 , where the liquid occupies the region
, where the liquid occupies the region 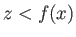 . The shape of the interface is assumed to be
. The shape of the interface is assumed to be  -independent. The unit normal to the interface (directed from liquid
to air) is thus
-independent. The unit normal to the interface (directed from liquid
to air) is thus
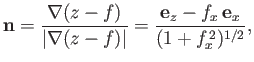 |
(3.25) |
where
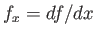 . Hence, the mean curvature of the interface is (Riley 1974)
. Hence, the mean curvature of the interface is (Riley 1974)
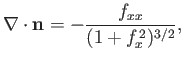 |
(3.26) |
where
 .
According to Equations (3.15) and (3.16), the shape of the interface is governed by the nonlinear differential
equation
.
According to Equations (3.15) and (3.16), the shape of the interface is governed by the nonlinear differential
equation
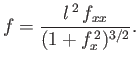 |
(3.27) |
where the vertical height, 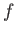 , of the interface
is measured relative to its equilibrium height in the absence of surface tension.
Multiplying the previous equation by
, of the interface
is measured relative to its equilibrium height in the absence of surface tension.
Multiplying the previous equation by
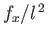 , and integrating with respect to
, and integrating with respect to  , we obtain
, we obtain
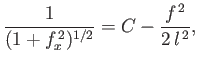 |
(3.28) |
where 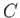 is a constant. It follows that
is a constant. It follows that
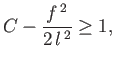 |
(3.29) |
and
![$\displaystyle \frac{1}{f_x} = \mp \frac{C-f^{\,2}/2\,l^{\,2}}{[1-(C-f^{\,2}/2\,l^{\,2})^2]^{1/2}}.$](img1165.png) |
(3.30) |
Figure:
Capillary curves for
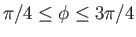 and (in order from the top to the bottom)
and (in order from the top to the bottom) 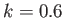 ,
, 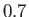 ,
, 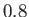 ,
, 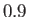 , and
, and 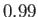 .
.
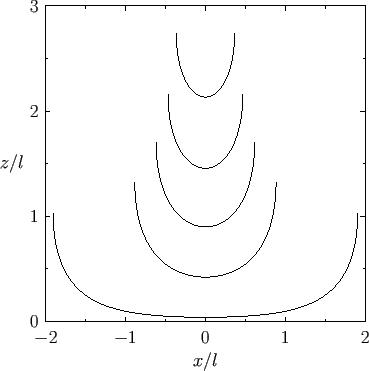 |
Let
 |
(3.31) |
where 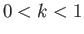 , and
, and
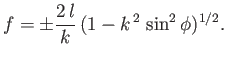 |
(3.32) |
Thus, from Equations (3.31) and (3.32),
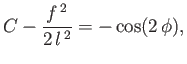 |
(3.33) |
and so the constraint (3.29) implies that
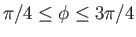 . Moreover, Equations (3.30)
and (3.33)
reduce to
. Moreover, Equations (3.30)
and (3.33)
reduce to
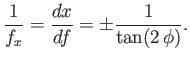 |
(3.34) |
It follows from Equations (3.32) and (3.34) that
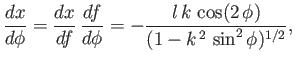 |
(3.35) |
which can be integrated to give
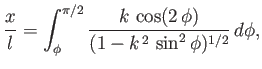 |
(3.36) |
assuming that  when
when
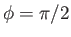 .
Thus, we get
.
Thus, we get
 |
(3.37) |
where
and
are types of incomplete elliptic integral (Abramowitz and Stegun 1965). In conclusion, the interface shape is determined parametrically by
where
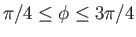 . Here, the parameter
. Here, the parameter 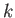 is restricted to lie in the range
is restricted to lie in the range 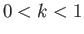 .
.
Figure:
Liquid/air interface for a liquid trapped between two vertical parallel plates located at  .
The contact angle of the interface with the plates is
.
The contact angle of the interface with the plates is
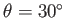 .
.
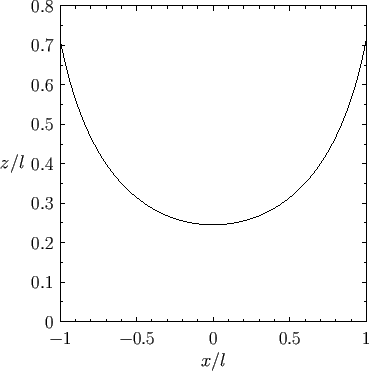 |
Figure 3.4 shows the capillary curves predicted by Equations (3.42) and (3.43) for various different values of 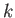 . Here, we have chosen the plus sign in Equation (3.43).
However, if the minus sign is chosen then
the curves are simply inverted: that is,
. Here, we have chosen the plus sign in Equation (3.43).
However, if the minus sign is chosen then
the curves are simply inverted: that is,
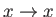 and
and
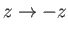 . In can be seen that
all of the curves shown in the figure are symmetric about
. In can be seen that
all of the curves shown in the figure are symmetric about  : that is,
: that is,
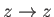 as
as
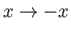 .
Consequently, we can use these curves to determine the shape of the liquid/air interface which arises when a liquid is trapped between
two flat vertical plates (made of the same material) that are parallel to one another. Suppose that the plates in question lie at
.
Consequently, we can use these curves to determine the shape of the liquid/air interface which arises when a liquid is trapped between
two flat vertical plates (made of the same material) that are parallel to one another. Suppose that the plates in question lie at  . Furthermore, let the angle of contact of the interface
with the plates be
. Furthermore, let the angle of contact of the interface
with the plates be 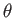 , where
, where
 . Because the angle of contact is acute, we expect the liquid to
be drawn upward between the plates, and the interface to be concave (from above). This corresponds to the
positive sign in Equation (3.43). In order for the interface to meet the plates at the correct angle, we require
. Because the angle of contact is acute, we expect the liquid to
be drawn upward between the plates, and the interface to be concave (from above). This corresponds to the
positive sign in Equation (3.43). In order for the interface to meet the plates at the correct angle, we require
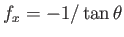 at
at 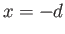 and
and
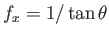 at
at 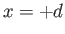 . However, if one of these boundary conditions is
satisfied then, by symmetry, the other is automatically satisfied.
From Equation (3.34) (choosing the positive sign), the latter boundary condition yields
. However, if one of these boundary conditions is
satisfied then, by symmetry, the other is automatically satisfied.
From Equation (3.34) (choosing the positive sign), the latter boundary condition yields
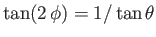 at
at 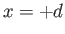 ,
which is equivalent to
,
which is equivalent to 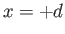 when
when
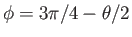 . Substituting this value of
. Substituting this value of 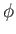 into Equation (3.42), we can numerically determine the
value of
into Equation (3.42), we can numerically determine the
value of 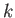 for which
for which 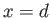 . The interface shape is then given by Equations (3.42) and (3.43), using
the aforementioned value of
. The interface shape is then given by Equations (3.42) and (3.43), using
the aforementioned value of 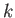 , and
, and 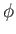 in the range
in the range
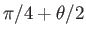 to
to
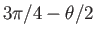 .
For instance, if
.
For instance, if 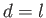 and
and
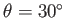 then
then  , and the associated interface is shown
in Figure 3.5. Furthermore, if we invert this interface (i.e.,
, and the associated interface is shown
in Figure 3.5. Furthermore, if we invert this interface (i.e.,
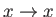 and
and
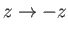 ) then
we obtain the interface which corresponds to the same plate spacing, but an obtuse contact angle of
) then
we obtain the interface which corresponds to the same plate spacing, but an obtuse contact angle of
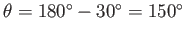 .
.
Consider the limit 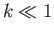 , which is such that the distance between the two plates is much less than the capillary
length. It is easily demonstrated that, at small
, which is such that the distance between the two plates is much less than the capillary
length. It is easily demonstrated that, at small 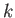 (Abramowitz and Stegun 1965)
(Abramowitz and Stegun 1965)
where
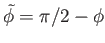 . Thus, Equations (3.42) and (3.43) reduce to
. Thus, Equations (3.42) and (3.43) reduce to
It follows that the interface is a segment of the curved surface of a cylinder whose axis runs parallel to the
 -axis. If the distance between the
plates is
-axis. If the distance between the
plates is 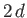 , and the contact angle is
, and the contact angle is 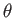 , then we require
, then we require 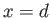 when
when
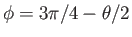 (which
corresponds to
(which
corresponds to
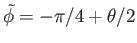 ).
From Equation (3.46), this constraint yields
).
From Equation (3.46), this constraint yields
 |
(3.48) |
Thus, the height that the liquid rises between the two plates--that is,
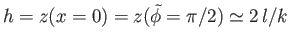 --is given by
--is given by
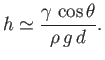 |
(3.49) |
This result is the form taken by Jurin's law, (3.23), for a liquid drawn up between two parallel plates
of spacing 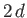 .
.
Figure:
Liquid/air interface for a liquid in contact with a vertical plate located at  .
The contact angle of the interface with the plate is
.
The contact angle of the interface with the plate is
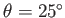 .
.
 |
Consider the case 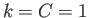 , which is such that the distance between the two plates is infinite. Let the leftmost plate
lie at
, which is such that the distance between the two plates is infinite. Let the leftmost plate
lie at  , and let us completely neglect the rightmost plate, because it lies at infinity. Suppose that
, and let us completely neglect the rightmost plate, because it lies at infinity. Suppose that 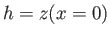 is the
height of the interface above the free surface of the liquid at the point where the interface meets the leftmost plate.
If
is the
height of the interface above the free surface of the liquid at the point where the interface meets the leftmost plate.
If 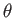 is the angle of contact of the interface with the plate then we require
is the angle of contact of the interface with the plate then we require
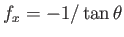 at
at  .
Because
.
Because 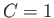 , it follows from Equation (3.28) that
, it follows from Equation (3.28) that
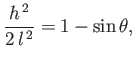 |
(3.50) |
or
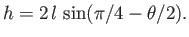 |
(3.51) |
Furthermore, again recalling that  , Equation (3.30) can be integrated to
give
, Equation (3.30) can be integrated to
give
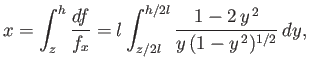 |
(3.52) |
where we have chosen the minus sign, and
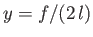 . Making the substitution
. Making the substitution 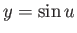 , this becomes
, this becomes
![$\displaystyle \frac{x}{l} = \int_{\sin^{-1}(z/2\,l)}^{\sin^{-1}(h/2\,l)}\left(\...
...cos u}{\sin u}\right)+2\,\cos u\right]_{\sin^{-1}(z/2\,l)}^{\sin^{-1}(h/2\,l)},$](img1228.png) |
(3.53) |
which reduces to
 |
(3.54) |
because
![$ \cosh^{-1}(z)\equiv \ln[z+(z^{\,2}-1)^{1/2}]$](img1230.png) . Thus, Equations (3.51) and (3.54)
specify the shape of a liquid/air interface that meets an isolated vertical plate at
. Thus, Equations (3.51) and (3.54)
specify the shape of a liquid/air interface that meets an isolated vertical plate at  . In particular,
Equation (3.51) gives the height that the interface climbs up the plate (relative to the free surface) due to the action of
surface tension. Note that this height is restricted to lie in the range
. In particular,
Equation (3.51) gives the height that the interface climbs up the plate (relative to the free surface) due to the action of
surface tension. Note that this height is restricted to lie in the range
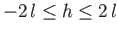 , irrespective
of the angle of contact.
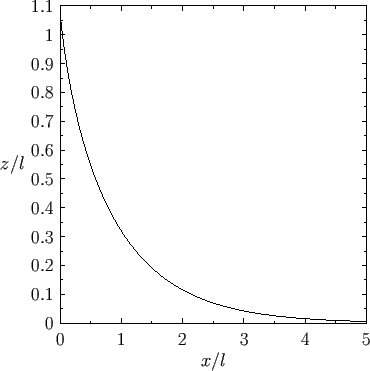
Figure 3.6 shows an example interface calculated for
, irrespective
of the angle of contact.
Figure 3.6 shows an example interface calculated for
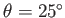 .
.



Next: Axisymmetric Soap-Bubbles
Up: Surface Tension
Previous: Jurin's Law
Richard Fitzpatrick
2016-01-22
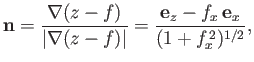
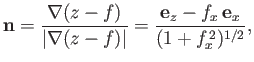
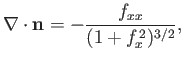
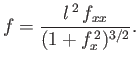
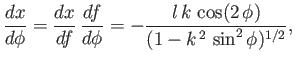
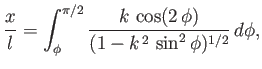


![]() . Here, we have chosen the plus sign in Equation (3.43).
However, if the minus sign is chosen then
the curves are simply inverted: that is,
. Here, we have chosen the plus sign in Equation (3.43).
However, if the minus sign is chosen then
the curves are simply inverted: that is,
![]() and
and
![]() . In can be seen that
all of the curves shown in the figure are symmetric about
. In can be seen that
all of the curves shown in the figure are symmetric about ![]() : that is,
: that is,
![]() as
as
![]() .
Consequently, we can use these curves to determine the shape of the liquid/air interface which arises when a liquid is trapped between
two flat vertical plates (made of the same material) that are parallel to one another. Suppose that the plates in question lie at
.
Consequently, we can use these curves to determine the shape of the liquid/air interface which arises when a liquid is trapped between
two flat vertical plates (made of the same material) that are parallel to one another. Suppose that the plates in question lie at ![]() . Furthermore, let the angle of contact of the interface
with the plates be
. Furthermore, let the angle of contact of the interface
with the plates be ![]() , where
, where
![]() . Because the angle of contact is acute, we expect the liquid to
be drawn upward between the plates, and the interface to be concave (from above). This corresponds to the
positive sign in Equation (3.43). In order for the interface to meet the plates at the correct angle, we require
. Because the angle of contact is acute, we expect the liquid to
be drawn upward between the plates, and the interface to be concave (from above). This corresponds to the
positive sign in Equation (3.43). In order for the interface to meet the plates at the correct angle, we require
![]() at
at ![]() and
and
![]() at
at ![]() . However, if one of these boundary conditions is
satisfied then, by symmetry, the other is automatically satisfied.
From Equation (3.34) (choosing the positive sign), the latter boundary condition yields
. However, if one of these boundary conditions is
satisfied then, by symmetry, the other is automatically satisfied.
From Equation (3.34) (choosing the positive sign), the latter boundary condition yields
![]() at
at ![]() ,
which is equivalent to
,
which is equivalent to ![]() when
when
![]() . Substituting this value of
. Substituting this value of ![]() into Equation (3.42), we can numerically determine the
value of
into Equation (3.42), we can numerically determine the
value of ![]() for which
for which ![]() . The interface shape is then given by Equations (3.42) and (3.43), using
the aforementioned value of
. The interface shape is then given by Equations (3.42) and (3.43), using
the aforementioned value of ![]() , and
, and ![]() in the range
in the range
![]() to
to
![]() .
For instance, if
.
For instance, if ![]() and
and
![]() then
then ![]() , and the associated interface is shown
in Figure 3.5. Furthermore, if we invert this interface (i.e.,
, and the associated interface is shown
in Figure 3.5. Furthermore, if we invert this interface (i.e.,
![]() and
and
![]() ) then
we obtain the interface which corresponds to the same plate spacing, but an obtuse contact angle of
) then
we obtain the interface which corresponds to the same plate spacing, but an obtuse contact angle of
![]() .
.
![]() , which is such that the distance between the two plates is much less than the capillary
length. It is easily demonstrated that, at small
, which is such that the distance between the two plates is much less than the capillary
length. It is easily demonstrated that, at small ![]() (Abramowitz and Stegun 1965)
(Abramowitz and Stegun 1965)
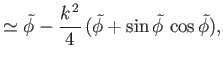
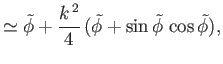

![$\displaystyle \simeq \frac{2}{k}-\frac{k}{2}\,[1-\cos(2\,\skew{5}\tilde{\phi})].$](img1213.png)

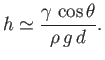

![]() , which is such that the distance between the two plates is infinite. Let the leftmost plate
lie at
, which is such that the distance between the two plates is infinite. Let the leftmost plate
lie at ![]() , and let us completely neglect the rightmost plate, because it lies at infinity. Suppose that
, and let us completely neglect the rightmost plate, because it lies at infinity. Suppose that ![]() is the
height of the interface above the free surface of the liquid at the point where the interface meets the leftmost plate.
If
is the
height of the interface above the free surface of the liquid at the point where the interface meets the leftmost plate.
If ![]() is the angle of contact of the interface with the plate then we require
is the angle of contact of the interface with the plate then we require
![]() at
at ![]() .
Because
.
Because ![]() , it follows from Equation (3.28) that
, it follows from Equation (3.28) that
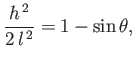
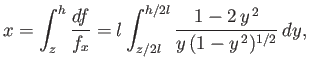
![$\displaystyle \frac{x}{l} = \int_{\sin^{-1}(z/2\,l)}^{\sin^{-1}(h/2\,l)}\left(\...
...cos u}{\sin u}\right)+2\,\cos u\right]_{\sin^{-1}(z/2\,l)}^{\sin^{-1}(h/2\,l)},$](img1228.png)