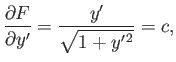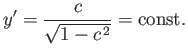Next: Conditional Variation
Up: Calculus of Variations
Previous: Indroduction
Euler-Lagrange Equation
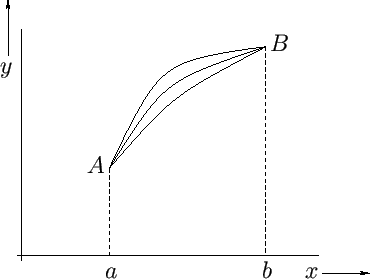
It is a well-known fact, first enunciated by Archimedes, that the shortest
distance between two points in a plane is a straight-line. However, suppose that
we wish to demonstrate this result from first principles. Let us consider the
length, 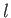 , of various curves,
, of various curves, 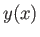 , which run between two fixed
points,
, which run between two fixed
points, 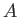 and
and 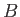 , in a plane, as illustrated in Figure E.1. Now,
, in a plane, as illustrated in Figure E.1. Now, 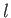 takes the form
takes the form
![$\displaystyle l = \int_A^B (dx^{\,2} + dy^{\,2})^{1/2} = \int_a^b [1 + y'^{\,2}(x)]^{1/2}\,dx,$](img7295.png) |
(E.1) |
where
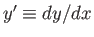 . Note that
. Note that 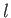 is a function of the function
is a function of the function 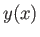 .
In mathematics, a function of a function is termed a functional.
.
In mathematics, a function of a function is termed a functional.
Figure:
Different paths between points 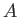 and
and 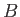 .
.
 |
In order to find the shortest path between points 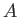 and
and 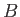 , we need to minimize the functional
, we need to minimize the functional  with respect to small variations
in the function
with respect to small variations
in the function 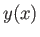 , subject to the constraint that the end points,
, subject to the constraint that the end points, 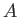 and
and 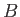 , remain fixed. In other words, we need to solve
, remain fixed. In other words, we need to solve
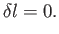 |
(E.2) |
The meaning of the previous equation is that if
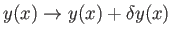 , where
, where
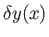 is small, then the first-order variation in
is small, then the first-order variation in 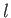 ,
denoted
,
denoted 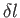 ,
vanishes. In other words,
,
vanishes. In other words,
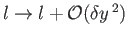 . The particular function
. The particular function
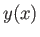 for which
for which
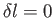 obviously yields an extremum of
obviously yields an extremum of 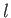 (i.e., either a maximum or a minimum). Hopefully,
in the case under consideration,
it yields a minimum of
(i.e., either a maximum or a minimum). Hopefully,
in the case under consideration,
it yields a minimum of 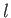 .
.
Consider a general functional of the form
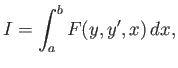 |
(E.3) |
where the end points of the integration are fixed.
Suppose that
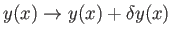 . The first-order variation in
. The first-order variation in  is written
is written
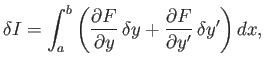 |
(E.4) |
where
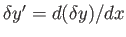 . Setting
. Setting 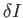 to zero, we
obtain
to zero, we
obtain
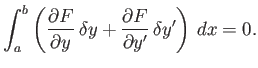 |
(E.5) |
This equation must be satisfied for all possible small perturbations
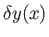 .
.
Integrating the second term in the integrand of the previous equation by
parts, we get
![$\displaystyle \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(...
...ight]\delta y\,dx +\left[\frac{\partial F}{\partial y'}\,\delta y\right]_a^b=0.$](img7310.png) |
(E.6) |
However, if the end points are fixed then
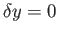 at
at
 and
and  . Hence, the last term on the left-hand side of the
previous equation is zero. Thus, we obtain
. Hence, the last term on the left-hand side of the
previous equation is zero. Thus, we obtain
![$\displaystyle \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)\right]\delta y\,dx =0.$](img7313.png) |
(E.7) |
The previous equation must be satisfied for all small perturbations
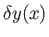 . The only way in which this is possible is for the
expression enclosed in square brackets in the integral to be zero. Hence, the functional
. The only way in which this is possible is for the
expression enclosed in square brackets in the integral to be zero. Hence, the functional
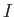 attains an extremum value whenever
attains an extremum value whenever
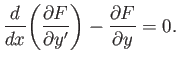 |
(E.8) |
This condition is known as the Euler-Lagrange equation.
Let us consider some special cases. Suppose that 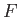 does not explicitly
depend on
does not explicitly
depend on  . It follows that
. It follows that
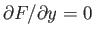 . Hence,
the Euler-Lagrange equation (E.8) simplifies to
. Hence,
the Euler-Lagrange equation (E.8) simplifies to
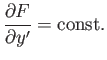 |
(E.9) |
Next, suppose that 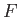 does not depend explicitly on
does not depend explicitly on  . Multiplying
Equation (E.8) by
. Multiplying
Equation (E.8) by 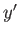 , we obtain
, we obtain
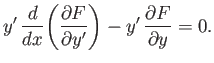 |
(E.10) |
However,
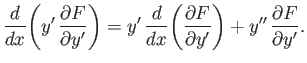 |
(E.11) |
Thus, we get
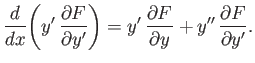 |
(E.12) |
Now, if 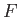 is not an explicit function of
is not an explicit function of  then the right-hand side of
the previous equation is the total derivative of
then the right-hand side of
the previous equation is the total derivative of 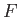 , namely
, namely 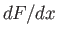 .
Hence, we obtain
.
Hence, we obtain
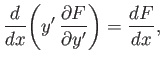 |
(E.13) |
which yields
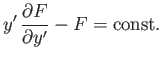 |
(E.14) |
Returning to the case under consideration, we have
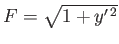 , according to Equation (E.1) and (E.3). Hence,
, according to Equation (E.1) and (E.3). Hence, 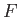 is not
an explicit function of
is not
an explicit function of  , so Equation (E.9) yields
, so Equation (E.9) yields
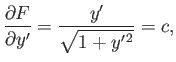 |
(E.15) |
where 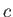 is a constant. So,
is a constant. So,
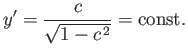 |
(E.16) |
Of course,
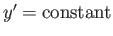 is the equation of a straight-line. Thus, the shortest distance between two fixed points in a plane is indeed a
straight-line.
is the equation of a straight-line. Thus, the shortest distance between two fixed points in a plane is indeed a
straight-line.



Next: Conditional Variation
Up: Calculus of Variations
Previous: Indroduction
Richard Fitzpatrick
2016-01-22
![$\displaystyle l = \int_A^B (dx^{\,2} + dy^{\,2})^{1/2} = \int_a^b [1 + y'^{\,2}(x)]^{1/2}\,dx,$](img7295.png)
![]() and
and ![]() , we need to minimize the functional
, we need to minimize the functional ![]() with respect to small variations
in the function
with respect to small variations
in the function ![]() , subject to the constraint that the end points,
, subject to the constraint that the end points, ![]() and
and ![]() , remain fixed. In other words, we need to solve
, remain fixed. In other words, we need to solve
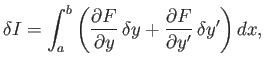
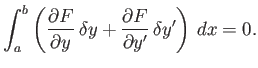
![$\displaystyle \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(...
...ight]\delta y\,dx +\left[\frac{\partial F}{\partial y'}\,\delta y\right]_a^b=0.$](img7310.png)
![$\displaystyle \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)\right]\delta y\,dx =0.$](img7313.png)
![]() does not explicitly
depend on
does not explicitly
depend on ![]() . It follows that
. It follows that
![]() . Hence,
the Euler-Lagrange equation (E.8) simplifies to
. Hence,
the Euler-Lagrange equation (E.8) simplifies to
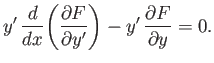
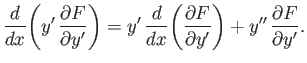
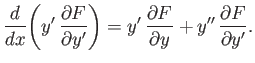
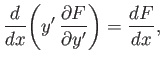
![]() , according to Equation (E.1) and (E.3). Hence,
, according to Equation (E.1) and (E.3). Hence, ![]() is not
an explicit function of
is not
an explicit function of ![]() , so Equation (E.9) yields
, so Equation (E.9) yields