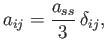Next: Exercises
Up: Cartesian Tensors
Previous: Tensor Fields
Isotropic Tensors
A tensor which has the special property that its components take the same value in all
Cartesian coordinate systems is called an isotropic tensor. We have already encountered two
such tensors: namely, the second-order identity tensor,
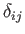 , and the third-order
permutation tensor,
, and the third-order
permutation tensor,
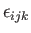 . Of course, all scalars are isotropic. Moreover, as is easily
demonstrated, there are
no isotropic vectors (other than the null vector).
It turns out that the
most general isotropic Cartesian tensors of second-, third-, and fourth-order are
. Of course, all scalars are isotropic. Moreover, as is easily
demonstrated, there are
no isotropic vectors (other than the null vector).
It turns out that the
most general isotropic Cartesian tensors of second-, third-, and fourth-order are
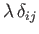 ,
,
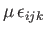 ,
and
,
and
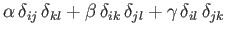 , respectively,
where
, respectively,
where 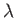 ,
,  ,
, 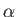 ,
, 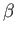 , and
, and 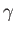 are scalars. Let us prove these important results (Hodge 1961).
are scalars. Let us prove these important results (Hodge 1961).
The most general second-order isotropic tensor,  , is such that
, is such that
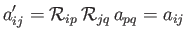 |
(B.65) |
for arbitrary rotations of the coordinate axes.
It follows from Equation (B.24) that, to first order in the
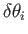 ,
,
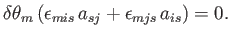 |
(B.66) |
However, the
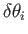 are arbitrary, so we can write
are arbitrary, so we can write
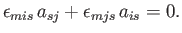 |
(B.67) |
Let us multiply by
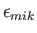 . With the aid of Equation (B.16), we obtain
. With the aid of Equation (B.16), we obtain
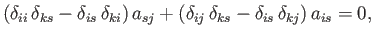 |
(B.68) |
which reduces to
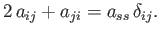 |
(B.69) |
Interchanging the labels 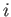 and
and 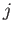 , and then taking the difference between the two equations thus obtained, we deduce that
, and then taking the difference between the two equations thus obtained, we deduce that
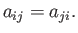 |
(B.70) |
Hence,
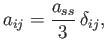 |
(B.71) |
which implies that
 |
(B.72) |
For the case of an isotropic third-order tensor, Equation (B.67) generalizes to
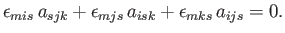 |
(B.73) |
Multiplying by
 ,
,
 , and
, and
 , and then
setting
, and then
setting  ,
, 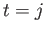 , and
, and 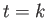 , respectively, we obtain
, respectively, we obtain
respectively. However, multiplying the previous equations by
 ,
,
 , and
, and
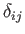 , and
then setting
, and
then setting 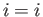 ,
, 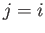 , and
, and  , respectively, we
obtain
, respectively, we
obtain
respectively,
which implies that
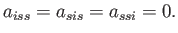 |
(B.80) |
Hence, we deduce that
The solution to the previous equation must satisfy
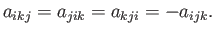 |
(B.84) |
This implies, from Equation (B.8), that
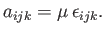 |
(B.85) |
For the case of an isotropic fourth-order tensor, Equation (B.73) generalizes to
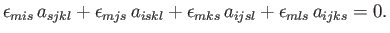 |
(B.86) |
Multiplying the previous by
 ,
,
 ,
,
 ,
,
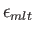 , and then
setting
, and then
setting  ,
, 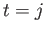 ,
, 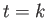 , and
, and 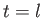 , respectively, we obtain
, respectively, we obtain
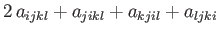 |
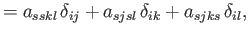 |
(B.87) |
 |
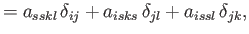 |
(B.88) |
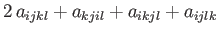 |
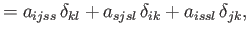 |
(B.89) |
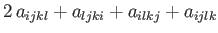 |
 |
(B.90) |
respectively.
Now, if 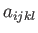 is an isotropic fourth-order tensor then
is an isotropic fourth-order tensor then  is clearly an isotropic second-order tensor, which means that is a multiple of
is clearly an isotropic second-order tensor, which means that is a multiple of
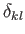 . This, and similar arguments, allows us to deduce that
. This, and similar arguments, allows us to deduce that
Let us assume, for the moment, that
Thus, we get
Relations of the form
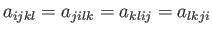 |
(B.101) |
can be obtained by subtracting the sum of one pair of Equations (B.97)-(B.100) from the sum of the other pair.
These relations justify Equations (B.94)-(B.96).
Equations (B.97) and (B.101) can be combined to give
The latter two equations are obtained from the first via cyclic permutation of 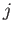 ,
, 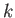 , and
, and 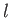 , with
, with 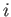 remaining unchanged.
Summing Equations (B.102)-(B.104), we get
remaining unchanged.
Summing Equations (B.102)-(B.104), we get
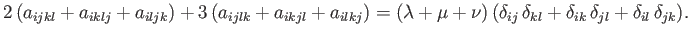 |
(B.105) |
It follows from symmetry that
 |
(B.106) |
This can be seen by swapping the indices 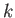 and
and 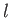 in the previous expression.
Finally, substitution into Equation (B.102) yields
in the previous expression.
Finally, substitution into Equation (B.102) yields
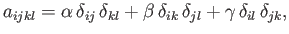 |
(B.107) |
where



Next: Exercises
Up: Cartesian Tensors
Previous: Tensor Fields
Richard Fitzpatrick
2016-01-22
![]() , is such that
, is such that