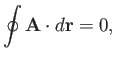Next: Grad Operator
Up: Vectors and Vector Fields
Previous: Volume Integrals
Gradient
A one-dimensional function 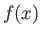 has a gradient
has a gradient 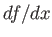 which is
defined as the slope of the tangent to the curve at
which is
defined as the slope of the tangent to the curve at  .
We wish to extend this idea to cover scalar fields in two and three dimensions.
.
We wish to extend this idea to cover scalar fields in two and three dimensions.
Consider a two-dimensional scalar field 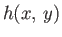 that represents (say) height above sea-level in a hilly region.
Let
that represents (say) height above sea-level in a hilly region.
Let
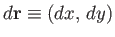 be an element of horizontal distance. Consider
be an element of horizontal distance. Consider
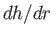 , where
, where 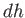 is the change in height after moving an infinitesimal distance
is the change in height after moving an infinitesimal distance
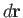 . This quantity is somewhat like the one-dimensional gradient, except that
. This quantity is somewhat like the one-dimensional gradient, except that
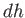 depends on the direction of
depends on the direction of 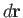 , as well as its magnitude.
In the immediate vicinity of some point
, as well as its magnitude.
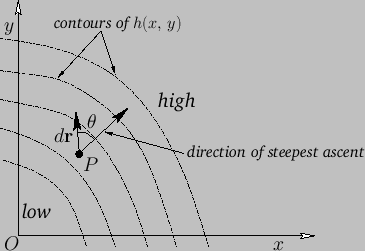
In the immediate vicinity of some point 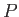 , the slope reduces to an inclined plane. (See Figure A.19.)
The largest value of
, the slope reduces to an inclined plane. (See Figure A.19.)
The largest value of 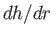 is straight up the slope. It is easily shown that for any other direction
is straight up the slope. It is easily shown that for any other direction
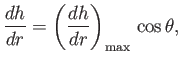 |
(A.103) |
where 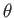 is the angle shown in Figure A.19.
Let us define a two-dimensional vector,
is the angle shown in Figure A.19.
Let us define a two-dimensional vector,
 ,
called the gradient of
,
called the gradient of 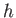 , whose magnitude is
, whose magnitude is
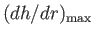 , and whose direction is the direction of steepest ascent.
The
, and whose direction is the direction of steepest ascent.
The
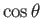 variation exhibited in the previous expression ensures that the component of
variation exhibited in the previous expression ensures that the component of
 in any
direction is equal to
in any
direction is equal to 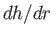 for that direction.
for that direction.
Figure A.19:
A two-dimensional gradient.
 |
The component of 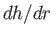 in the
in the  -direction can be obtained by plotting out the
profile of
-direction can be obtained by plotting out the
profile of 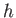 at constant
at constant  , and then finding the slope of the tangent to the
curve at given
, and then finding the slope of the tangent to the
curve at given  . This quantity is known as the partial derivative of
. This quantity is known as the partial derivative of
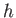 with respect to
with respect to  at constant
at constant  , and is denoted
, and is denoted
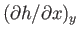 .
Likewise, the gradient of the profile at constant
.
Likewise, the gradient of the profile at constant  is written
is written
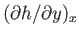 . Note that the subscripts denoting constant
. Note that the subscripts denoting constant  and
constant
and
constant  are usually omitted, unless there is any ambiguity. It follows that
in component form
are usually omitted, unless there is any ambiguity. It follows that
in component form
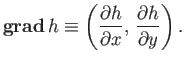 |
(A.104) |
Now, the equation of the tangent plane at
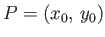 is
is
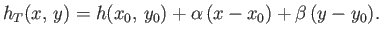 |
(A.105) |
This has the same local gradients as 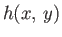 , so
, so
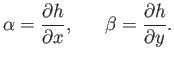 |
(A.106) |
For small 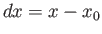 and
and 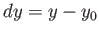 , the function
, the function 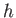 is coincident with the tangent
plane. It follows that
is coincident with the tangent
plane. It follows that
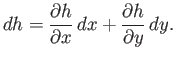 |
(A.107) |
But,
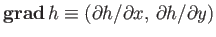 and
and
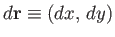 , so
, so
 |
(A.108) |
Incidentally, the previous equation demonstrates that
 is a proper vector,
because the left-hand side is a scalar, and, according to the properties of the dot
product, the right-hand side is also a scalar provided that
is a proper vector,
because the left-hand side is a scalar, and, according to the properties of the dot
product, the right-hand side is also a scalar provided that 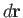 and
and
 are both
proper vectors (
are both
proper vectors (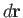 is an obvious vector, because it is
directly derived from displacements).
is an obvious vector, because it is
directly derived from displacements).
Consider, now, a three-dimensional temperature distribution
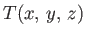 in
(say) a
reaction vessel. Let us define
in
(say) a
reaction vessel. Let us define
 , as before, as a vector whose magnitude is
, as before, as a vector whose magnitude is
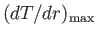 ,
and whose direction is the direction of the maximum gradient.
This vector is written in component form
,
and whose direction is the direction of the maximum gradient.
This vector is written in component form
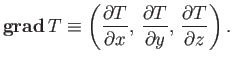 |
(A.109) |
Here,
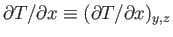 is the
gradient of the one-dimensional temperature profile at constant
is the
gradient of the one-dimensional temperature profile at constant  and
and 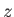 .
The change in
.
The change in 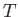 in going from point
in going from point 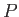 to a neighboring point offset by
to a neighboring point offset by
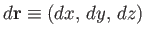 is
is
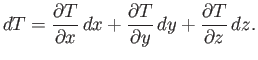 |
(A.110) |
In vector form, this becomes
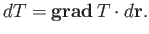 |
(A.111) |
Suppose that 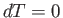 for some
for some 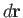 . It follows that
. It follows that
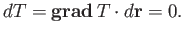 |
(A.112) |
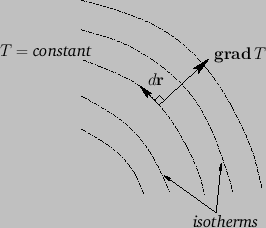
So, 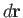 is perpendicular to
is perpendicular to
 . Because
. Because 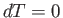 along so-called
``isotherms'' (i.e., contours of the temperature), we conclude that the isotherms
(contours) are everywhere perpendicular to
along so-called
``isotherms'' (i.e., contours of the temperature), we conclude that the isotherms
(contours) are everywhere perpendicular to
 . (See Figure A.20.)
. (See Figure A.20.)
Figure A.20:
Isotherms.
 |
It is, of course, possible to integrate 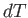 . For instance, the line integral of
. For instance, the line integral of 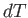 between points
between points 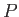 and
and
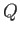 is written
is written
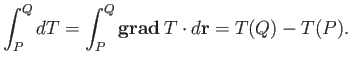 |
(A.113) |
This integral is clearly independent of the path taken between 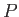 and
and 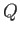 , so
, so
 must be path independent.
must be path independent.
Consider a vector field
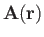 . In general, the line integral
. In general, the line integral
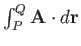 depends on the path
taken between the end points. However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if
depends on the path
taken between the end points. However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if 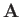 is a
conservative field then
is a
conservative field then
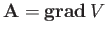 for some scalar field
for some scalar field 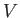 .
The proof of this is straightforward. Keeping
.
The proof of this is straightforward. Keeping 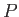 fixed, we have
fixed, we have
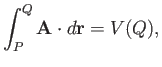 |
(A.114) |
where 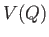 is a well-defined function, due to the path independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount
is a well-defined function, due to the path independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount 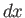 in the
in the  -direction. We have
-direction. We have
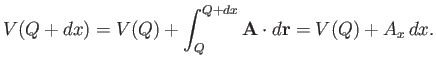 |
(A.115) |
Hence,
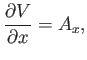 |
(A.116) |
with analogous relations for the other components of 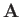 . It follows that
. It follows that
 |
(A.117) |
The force field due to gravity is a good example of a conservative field.
Now, if
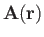 is a force-field then
is a force-field then
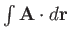 is the work done
in traversing some path. If
is the work done
in traversing some path. If 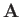 is conservative then
is conservative then
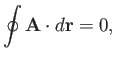 |
(A.118) |
where 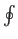 corresponds to the line integral around a closed loop.
The fact that zero net work is done in going around a closed loop is equivalent
to the conservation of energy (which is why conservative fields are called
``conservative''). A good example of a non-conservative field is the force field due
to friction. Clearly, a frictional system loses energy in going around a closed
cycle, so
corresponds to the line integral around a closed loop.
The fact that zero net work is done in going around a closed loop is equivalent
to the conservation of energy (which is why conservative fields are called
``conservative''). A good example of a non-conservative field is the force field due
to friction. Clearly, a frictional system loses energy in going around a closed
cycle, so
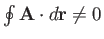 .
.



Next: Grad Operator
Up: Vectors and Vector Fields
Previous: Volume Integrals
Richard Fitzpatrick
2016-01-22
![]() that represents (say) height above sea-level in a hilly region.
Let
that represents (say) height above sea-level in a hilly region.
Let
![]() be an element of horizontal distance. Consider
be an element of horizontal distance. Consider
![]() , where
, where ![]() is the change in height after moving an infinitesimal distance
is the change in height after moving an infinitesimal distance
![]() . This quantity is somewhat like the one-dimensional gradient, except that
. This quantity is somewhat like the one-dimensional gradient, except that
![]() depends on the direction of
depends on the direction of ![]() , as well as its magnitude.
In the immediate vicinity of some point
, as well as its magnitude.
In the immediate vicinity of some point ![]() , the slope reduces to an inclined plane. (See Figure A.19.)
The largest value of
, the slope reduces to an inclined plane. (See Figure A.19.)
The largest value of ![]() is straight up the slope. It is easily shown that for any other direction
is straight up the slope. It is easily shown that for any other direction
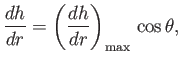
![]() in the
in the ![]() -direction can be obtained by plotting out the
profile of
-direction can be obtained by plotting out the
profile of ![]() at constant
at constant ![]() , and then finding the slope of the tangent to the
curve at given
, and then finding the slope of the tangent to the
curve at given ![]() . This quantity is known as the partial derivative of
. This quantity is known as the partial derivative of
![]() with respect to
with respect to ![]() at constant
at constant ![]() , and is denoted
, and is denoted
![]() .
Likewise, the gradient of the profile at constant
.
Likewise, the gradient of the profile at constant ![]() is written
is written
![]() . Note that the subscripts denoting constant
. Note that the subscripts denoting constant ![]() and
constant
and
constant ![]() are usually omitted, unless there is any ambiguity. It follows that
in component form
are usually omitted, unless there is any ambiguity. It follows that
in component form
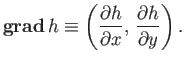
![]() is
is
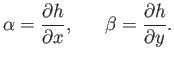
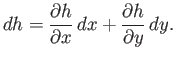
![]() in
(say) a
reaction vessel. Let us define
in
(say) a
reaction vessel. Let us define
![]() , as before, as a vector whose magnitude is
, as before, as a vector whose magnitude is
![]() ,
and whose direction is the direction of the maximum gradient.
This vector is written in component form
,
and whose direction is the direction of the maximum gradient.
This vector is written in component form
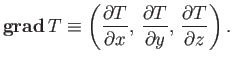
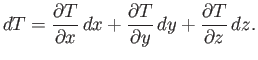
![]() . For instance, the line integral of
. For instance, the line integral of ![]() between points
between points ![]() and
and
![]() is written
is written
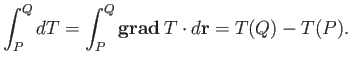
![]() . In general, the line integral
. In general, the line integral
![]() depends on the path
taken between the end points. However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if
depends on the path
taken between the end points. However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if ![]() is a
conservative field then
is a
conservative field then
![]() for some scalar field
for some scalar field ![]() .
The proof of this is straightforward. Keeping
.
The proof of this is straightforward. Keeping ![]() fixed, we have
fixed, we have
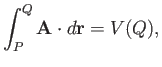
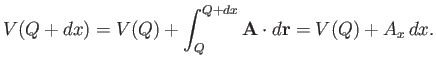
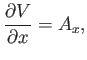
![]() is a force-field then
is a force-field then
![]() is the work done
in traversing some path. If
is the work done
in traversing some path. If ![]() is conservative then
is conservative then