


Next: Vector Product
Up: Vectors and Vector Fields
Previous: Scalar Product
Vector Area
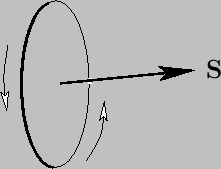
Suppose that we have planar surface of scalar area  . We can define a vector
area
. We can define a vector
area  whose magnitude is
whose magnitude is  , and whose direction is perpendicular to
the plane, in the sense determined by a right-hand circulation rule (see Section A.8) applied to the rim, assuming that a direction of circulation around the rim is specified. (See Figure A.7.)
This quantity clearly possesses both magnitude and direction. But is it a true
vector? We know that if the normal to the surface makes an angle
, and whose direction is perpendicular to
the plane, in the sense determined by a right-hand circulation rule (see Section A.8) applied to the rim, assuming that a direction of circulation around the rim is specified. (See Figure A.7.)
This quantity clearly possesses both magnitude and direction. But is it a true
vector? We know that if the normal to the surface makes an angle 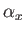 with
the
with
the  -axis then the area seen looking along the
-axis then the area seen looking along the  -direction is
-direction is
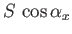 .
This is the
.
This is the  -component of
-component of  (because
(because
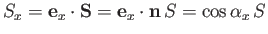 ,
where
,
where 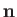 is the unit normal to the surface).
Similarly, if the normal makes an angle
is the unit normal to the surface).
Similarly, if the normal makes an angle 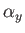 with the
with the  -axis then the
area seen looking along the
-axis then the
area seen looking along the  -direction is
-direction is
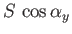 .
This is the
.
This is the  -component of
-component of  . If we limit ourselves to a surface whose
normal is perpendicular to the
. If we limit ourselves to a surface whose
normal is perpendicular to the  -direction then
-direction then
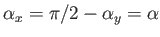 .
It follows that
.
It follows that
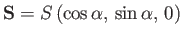 . If we rotate the
basis about the
. If we rotate the
basis about the
 -axis by
-axis by 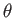 degrees, which is equivalent to rotating the normal to
the surface about the
degrees, which is equivalent to rotating the normal to
the surface about the  -axis by
-axis by 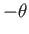 degrees, so that
degrees, so that
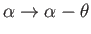 , then
, then
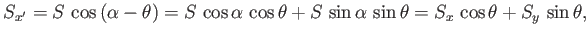 |
(A.33) |
which is the correct transformation rule for the  -component of a vector. The
other components transform correctly as well. This proves both
that a vector area is a
true vector, and that the components of a vector area are the projected areas seen looking
down the coordinate axes.
-component of a vector. The
other components transform correctly as well. This proves both
that a vector area is a
true vector, and that the components of a vector area are the projected areas seen looking
down the coordinate axes.
Figure A.7:
A vector area.
 |
According to the vector addition theorem, the projected area of two plane surfaces,
joined together at a line,
looking along the  -direction (say) is the
-direction (say) is the  -component of the resultant of the vector areas of the two surfaces.
Likewise, for many joined-up plane areas, the net area seen looking down the
-component of the resultant of the vector areas of the two surfaces.
Likewise, for many joined-up plane areas, the net area seen looking down the  -axis,
which is the same as the area of the outer rim seen looking down the
-axis,
which is the same as the area of the outer rim seen looking down the  -axis, is the
-axis, is the
 -component of the resultant of all the vector areas: that is,
-component of the resultant of all the vector areas: that is,
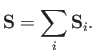 |
(A.34) |
If we approach a limit,
by letting the number of plane facets increase, and their areas reduce, then we
obtain a continuous surface denoted by the resultant vector area
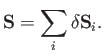 |
(A.35) |
It is
clear that the area of the rim seen looking down the  -axis is just
-axis is just 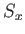 . Similarly, for the areas
of the rim seen looking down the other coordinate axes.
Note that it is the rim of the surface that determines the vector area, rather than the nature of
the surface spanning the rim. So, two different surfaces sharing the same rim both possess the same
vector area.
. Similarly, for the areas
of the rim seen looking down the other coordinate axes.
Note that it is the rim of the surface that determines the vector area, rather than the nature of
the surface spanning the rim. So, two different surfaces sharing the same rim both possess the same
vector area.
In conclusion, a loop (not all in one plane) has a vector area  which
is the resultant of the component vector areas of any surface ending on the loop. The
components of
which
is the resultant of the component vector areas of any surface ending on the loop. The
components of  are the areas of the loop seen looking down the coordinate axes. As a corollary, a closed surface has
are the areas of the loop seen looking down the coordinate axes. As a corollary, a closed surface has
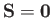 ,
because it does not possess a rim.
,
because it does not possess a rim.



Next: Vector Product
Up: Vectors and Vector Fields
Previous: Scalar Product
Richard Fitzpatrick
2016-01-22
![]() -direction (say) is the
-direction (say) is the ![]() -component of the resultant of the vector areas of the two surfaces.
Likewise, for many joined-up plane areas, the net area seen looking down the
-component of the resultant of the vector areas of the two surfaces.
Likewise, for many joined-up plane areas, the net area seen looking down the ![]() -axis,
which is the same as the area of the outer rim seen looking down the
-axis,
which is the same as the area of the outer rim seen looking down the ![]() -axis, is the
-axis, is the
![]() -component of the resultant of all the vector areas: that is,
-component of the resultant of all the vector areas: that is,
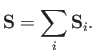
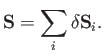
![]() which
is the resultant of the component vector areas of any surface ending on the loop. The
components of
which
is the resultant of the component vector areas of any surface ending on the loop. The
components of ![]() are the areas of the loop seen looking down the coordinate axes. As a corollary, a closed surface has
are the areas of the loop seen looking down the coordinate axes. As a corollary, a closed surface has
![]() ,
because it does not possess a rim.
,
because it does not possess a rim.