Next: Exercises
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Linearized Supersonic Flow
In Section 15.9, we found that the pressure coefficients on the upper and lower surfaces of a thin, flat airfoil of infinite span, inclined at a small angle of attack, 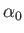 , to
uniform supersonic flow of Mach number
, to
uniform supersonic flow of Mach number
 , are
, are
respectively, where
 |
(15.198) |
Of course, a realistic airfoil has a finite span. The aim of this section is to investigate the effect of finite span on the lift developed by a flat airfoil.
Figure:
A rectangular airfoil of finite span. Here,
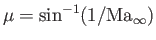 is the Mach angle, and
is the Mach angle, and
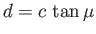 .
.
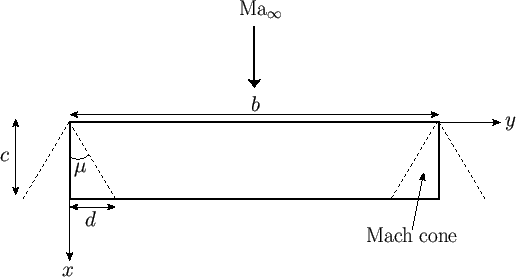 |
Suppose that the airfoil is rectangular, with span  , and width
, and width 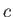 , as shown in Figure 15.13. The unperturbed
flow is parallel to the
, as shown in Figure 15.13. The unperturbed
flow is parallel to the  -axis, and the airfoil is inclined at a small angle
-axis, and the airfoil is inclined at a small angle 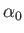 to the plane
to the plane  .
Because of the limited regions of influence in supersonic flow, the fact that the span is finite is only felt
within the Mach cones emanating from the two leading-edge corners of the airfoil.
This implies that the two-dimensional results (15.196) and
(15.197) are applicable everywhere on the airfoil surface, except inside the two Mach cones. In other
words, the inner part of the airfoil, lying between the two cones, behaves as if it were
part of an airfoil of infinite span.
.
Because of the limited regions of influence in supersonic flow, the fact that the span is finite is only felt
within the Mach cones emanating from the two leading-edge corners of the airfoil.
This implies that the two-dimensional results (15.196) and
(15.197) are applicable everywhere on the airfoil surface, except inside the two Mach cones. In other
words, the inner part of the airfoil, lying between the two cones, behaves as if it were
part of an airfoil of infinite span.
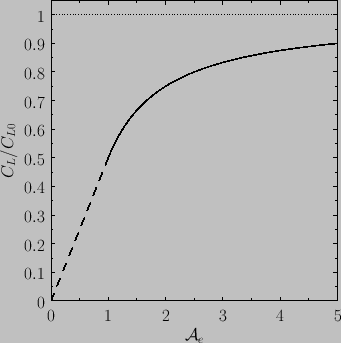
Assuming that the left-most leading-edge corner lies at the origin, the
pressure coefficient on the upper surface of the airfoil in the left-most Mach cone can be shown to take the form (Milne-Thompson 1958)
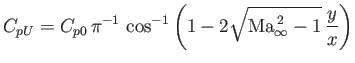 |
(15.199) |
for
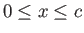 and
and
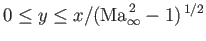 .
The corresponding pressure coefficient on the lower surface of the airfoil is written
.
The corresponding pressure coefficient on the lower surface of the airfoil is written
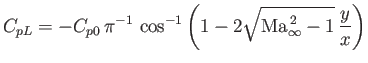 |
(15.200) |
for
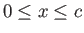 and
and
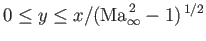 . There are analogous expressions for the pressure coefficients in the
right-most Mach cone.
The variation of the pressure coefficient along the span of a finite, flat airfoil is illustrated in Figure 15.14.
. There are analogous expressions for the pressure coefficients in the
right-most Mach cone.
The variation of the pressure coefficient along the span of a finite, flat airfoil is illustrated in Figure 15.14.
Figure:
Variation of the pressure coefficient along the span of a finite, flat airfoil of aspect-ratio 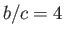 , placed in supersonic flow of
Mach number
, placed in supersonic flow of
Mach number
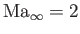 . The solid and dotted curves corresponds to
. The solid and dotted curves corresponds to  and
and 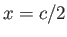 , respectively.
, respectively.
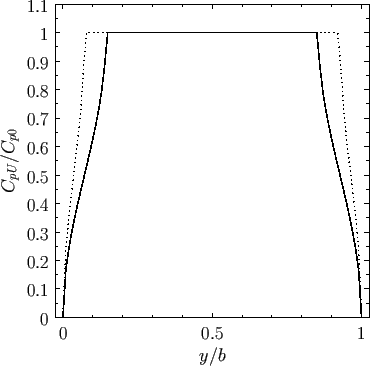 |
Note that
which implies that the average pressure coefficient inside the two Mach cones on the upper surface of the airfoil is 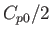 . Similarly,
the average pressure coefficient inside the Mach cones on the lower surface is
. Similarly,
the average pressure coefficient inside the Mach cones on the lower surface is 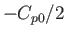 .
Thus, the coefficient of lift of the whole airfoil is less than the two-dimensional value,
.
Thus, the coefficient of lift of the whole airfoil is less than the two-dimensional value, 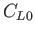 , by an amount
, by an amount
![$\displaystyle {\mit\Delta}C_L = \frac{(1/2)\,C_{L0}\,[(1/2)\,c\,d + (1/2)\,c\,d]}{c\,b}=\frac{(1/2)\,C_{L0}}{b/d} = \frac{(1/2)\,C_{L0}}{(b/c)\,(c/d)}.$](img6074.png) |
(15.202) |
The terms in the denominator are
where 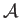 is termed the aspect-ratio of the airfoil. The previous three equations can be combined to give
is termed the aspect-ratio of the airfoil. The previous three equations can be combined to give
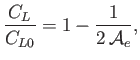 |
(15.205) |
where
 |
(15.206) |
is termed the effective aspect-ratio of the airfoil. Figure 15.15 shows the loss of
lift of a flat airfoil as a function of the effective aspect-ratio. Expression (15.205)
is valid for values of
 as small as unity (which corresponds to the case where
the Mach cones emanating from each leading-edge corner are just beginning to intersect the opposite side of the airfoil). For lower values of
as small as unity (which corresponds to the case where
the Mach cones emanating from each leading-edge corner are just beginning to intersect the opposite side of the airfoil). For lower values of
 , the
expression is different, but tends to zero, as indicated by the broken lin in the figure.
, the
expression is different, but tends to zero, as indicated by the broken lin in the figure.
Figure 15.15:
Loss of lift due to the finite span of a flat airfoil.
 |



Next: Exercises
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Linearized Supersonic Flow
Richard Fitzpatrick
2016-01-22

![]() , and width
, and width ![]() , as shown in Figure 15.13. The unperturbed
flow is parallel to the
, as shown in Figure 15.13. The unperturbed
flow is parallel to the ![]() -axis, and the airfoil is inclined at a small angle
-axis, and the airfoil is inclined at a small angle ![]() to the plane
to the plane ![]() .
Because of the limited regions of influence in supersonic flow, the fact that the span is finite is only felt
within the Mach cones emanating from the two leading-edge corners of the airfoil.
This implies that the two-dimensional results (15.196) and
(15.197) are applicable everywhere on the airfoil surface, except inside the two Mach cones. In other
words, the inner part of the airfoil, lying between the two cones, behaves as if it were
part of an airfoil of infinite span.
.
Because of the limited regions of influence in supersonic flow, the fact that the span is finite is only felt
within the Mach cones emanating from the two leading-edge corners of the airfoil.
This implies that the two-dimensional results (15.196) and
(15.197) are applicable everywhere on the airfoil surface, except inside the two Mach cones. In other
words, the inner part of the airfoil, lying between the two cones, behaves as if it were
part of an airfoil of infinite span.
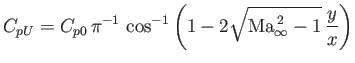
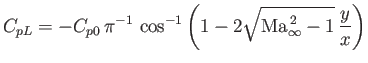




![$\displaystyle {\mit\Delta}C_L = \frac{(1/2)\,C_{L0}\,[(1/2)\,c\,d + (1/2)\,c\,d]}{c\,b}=\frac{(1/2)\,C_{L0}}{b/d} = \frac{(1/2)\,C_{L0}}{(b/c)\,(c/d)}.$](img6074.png)