


Next: Linearized Supersonic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Flow Past a
The aim of this section is to modify the two-dimensional, incompressible, subsonic aerodynamic theory discussed in Chapter 9 so as to take the finite compressibility of
air into account.
Consider compressible, subsonic flow over a thin airfoil at a small angle of attack. Such a situation can be analyzed using the small-perturbation theory
introduced in Section 15.12. As before, the unperturbed flow is of uniform speed 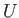 , directed parallel to the
, directed parallel to the  -axis, and the associated Mach number is
-axis, and the associated Mach number is
 .
The perturbed flow, due to the presence of the airfoil, is governed by Equation (15.127), which can be written in the elliptic
form (see Section 15.13)
.
The perturbed flow, due to the presence of the airfoil, is governed by Equation (15.127), which can be written in the elliptic
form (see Section 15.13)
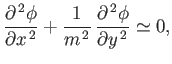 |
(15.164) |
where
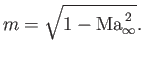 |
(15.165) |
Equation (15.164) can be transformed into a familiar incompressible form by introducing a transformed coordinate system
 , such
that
, such
that
In this transformed space, we define a transformed perturbed velocity potential,
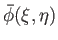 , such that
, such that
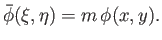 |
(15.168) |
Now,
so
It follows that
Thus, Equation (15.164) transforms to give
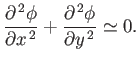 |
(15.173) |
However, this is simply Laplace's equation, which governs incompressible flow. (See Section 4.15.) Hence,
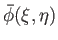 represents an incompressible flow in
represents an incompressible flow in
 space that is related to a
compressible flow, represented by
space that is related to a
compressible flow, represented by 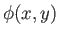 , in
, in 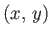 space.
space.
Suppose that the surface of the airfoil is given by  in
in 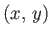 space, and
space, and
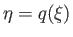 in
in
 space.
According to Equation (15.129), the boundary condition on the flow at the airfoil surface is
space.
According to Equation (15.129), the boundary condition on the flow at the airfoil surface is
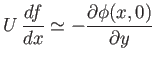 |
(15.174) |
in 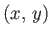 space. The analogous boundary condition in
space. The analogous boundary condition in
 space is
space is
 |
(15.175) |
However,
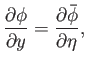 |
(15.176) |
which implies that
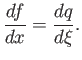 |
(15.177) |
In other words, the shape of the airfoil in ( ,
, ) space is the same as that in (
) space is the same as that in (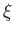 ,
,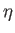 ) space. Hence, the
coordinate transformation
) space. Hence, the
coordinate transformation
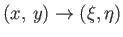 transforms compressible flow over an
airfoil in
transforms compressible flow over an
airfoil in 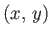 space to incompressible flow over the same airfoil in
space to incompressible flow over the same airfoil in
 space.
space.
According to Equation (15.128), the pressure coefficient in 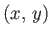 space is
written
space is
written
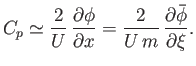 |
(15.178) |
The corresponding incompressible pressure coefficient in
 space is
space is
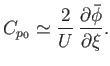 |
(15.179) |
A comparison of the previous two equations reveals that
 |
(15.180) |
This result is known as the Prandtl-Glauert rule: it is a similarity rule that relates incompressible flow over a
given two-dimensional airfoil to subsonic compressible flow over the same airfoil. Given that the
coefficient of lift is directly related to the pressure coefficient (see Section 15.9), we can also
deduce that
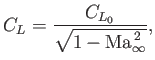 |
(15.181) |
where  is the coefficient of lift for compressible flow, and
is the coefficient of lift for compressible flow, and  the corresponding coefficient for
incompressible flow. It is clear that compressibility has the effect of increasing the lift on a given airfoil.
the corresponding coefficient for
incompressible flow. It is clear that compressibility has the effect of increasing the lift on a given airfoil.
Equation (15.181) indicates that the coefficient of lift goes to infinity as
 approaches
unity, which is an impossible result. The quandary is resolved by recalling that linearized theory breaks
down in the transonic regime (where
approaches
unity, which is an impossible result. The quandary is resolved by recalling that linearized theory breaks
down in the transonic regime (where
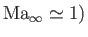 . In fact, the Prandlt-Glauert rule
is only accurate up to Mach numbers of approximately
. In fact, the Prandlt-Glauert rule
is only accurate up to Mach numbers of approximately 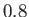 .
.
The effect of compressibility on subsonic flow-fields can be seen by noting that
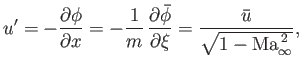 |
(15.182) |
where
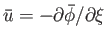 is the incompressible velocity perturbation parallel to the unperturbed flow.
It can be seen that as
is the incompressible velocity perturbation parallel to the unperturbed flow.
It can be seen that as
 increases, the parallel velocity perturbation,
increases, the parallel velocity perturbation, 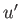 , also increases relative to
, also increases relative to 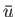 .
In other words, compressibility strengthens the disturbance of the flow introduced by the airfoil.
.
In other words, compressibility strengthens the disturbance of the flow introduced by the airfoil.
In conventional inviscid, incompressible aerodynamic theory, a two-dimensional airfoil experiences zero
aerodynamic drag (assuming that there is no separation of the boundary layer). (See Chapters 8 and 9.)
This is due to the fact that, in the absence of friction, the pressure distributions over the forward and rearward portions
of the airfoil exactly cancel in the direction of the unperturbed flow. Note that the compressible pressure
coefficient, 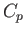 , only differs from the incompressible pressure coefficient,
, only differs from the incompressible pressure coefficient, 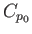 , by a constant scale-factor.
Thus, if the distribution of
, by a constant scale-factor.
Thus, if the distribution of 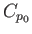 over the surface of the airfoil results in zero drag then the distribution of
over the surface of the airfoil results in zero drag then the distribution of
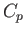 will also result in zero drag. In other words, in subsonic flow, compressibility does not give rise to additional
aerodynamic drag.
will also result in zero drag. In other words, in subsonic flow, compressibility does not give rise to additional
aerodynamic drag.



Next: Linearized Supersonic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Flow Past a
Richard Fitzpatrick
2016-01-22
![]() , directed parallel to the
, directed parallel to the ![]() -axis, and the associated Mach number is
-axis, and the associated Mach number is
![]() .
The perturbed flow, due to the presence of the airfoil, is governed by Equation (15.127), which can be written in the elliptic
form (see Section 15.13)
.
The perturbed flow, due to the presence of the airfoil, is governed by Equation (15.127), which can be written in the elliptic
form (see Section 15.13)
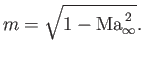
![]() , such
that
, such
that

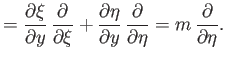
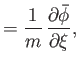
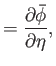
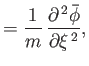
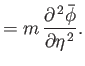
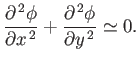
![]() in
in ![]() space, and
space, and
![]() in
in
![]() space.
According to Equation (15.129), the boundary condition on the flow at the airfoil surface is
space.
According to Equation (15.129), the boundary condition on the flow at the airfoil surface is
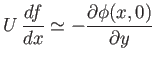

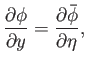
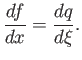
![]() space is
written
space is
written
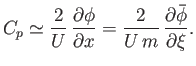
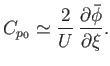

![]() approaches
unity, which is an impossible result. The quandary is resolved by recalling that linearized theory breaks
down in the transonic regime (where
approaches
unity, which is an impossible result. The quandary is resolved by recalling that linearized theory breaks
down in the transonic regime (where
![]() . In fact, the Prandlt-Glauert rule
is only accurate up to Mach numbers of approximately
. In fact, the Prandlt-Glauert rule
is only accurate up to Mach numbers of approximately ![]() .
.
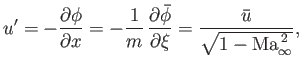
![]() , only differs from the incompressible pressure coefficient,
, only differs from the incompressible pressure coefficient, ![]() , by a constant scale-factor.
Thus, if the distribution of
, by a constant scale-factor.
Thus, if the distribution of ![]() over the surface of the airfoil results in zero drag then the distribution of
over the surface of the airfoil results in zero drag then the distribution of
![]() will also result in zero drag. In other words, in subsonic flow, compressibility does not give rise to additional
aerodynamic drag.
will also result in zero drag. In other words, in subsonic flow, compressibility does not give rise to additional
aerodynamic drag.