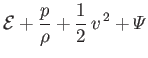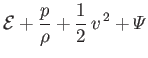Next: Mach Number
Up: One-Dimensional Compressible Inviscid Flow
Previous: Sound Waves
Bernoulli's Theorem
According to Bernoulli's theorem, which was introduced in Section 4.3, the quantity
 is constant
along a streamline in steady inviscid flow, where
is constant
along a streamline in steady inviscid flow, where 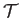 is the total energy per unit mass. For the case of a compressible
fluid,
is the total energy per unit mass. For the case of a compressible
fluid,
 . Hence, we deduce that
. Hence, we deduce that
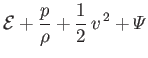 |
(14.53) |
is constant along a streamline. In particular, for an ideal gas, we find that
 |
(14.54) |
is constant along a streamline, where use has been made of Equation (14.18).
Consider a solid object moving through an ideal gas. Generally speaking, there is at least one stagnation point in front of the object, where the gas comes to rest
relative to it. At this point, the gas is adiabatically compressed, and there is an associated rise in temperature.
In the frame of reference in which the object is at rest, and the gas a long way from it moves with constant speed and
temperature, application of Bernoulli's theorem yields
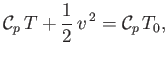 |
(14.55) |
where 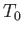 is the stagnation-point temperature, and
is the stagnation-point temperature, and  the temperature at some general point where the flow speed is
the temperature at some general point where the flow speed is 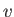 .
Thus, the total temperature rise due to adiabatic compression is
.
Thus, the total temperature rise due to adiabatic compression is
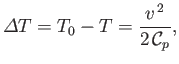 |
(14.56) |
where 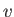 and
and  are the asymptotic flow speed and temperature, respectively.
It can be seen that the stagnation temperature rise only depends on the velocity difference between the object and the gas, and is
independent of the gas's density, temperature, or pressure. Note, however, that a lower molar mass implies a
higher specific heat, and, hence, a smaller stagnation temperature rise.
are the asymptotic flow speed and temperature, respectively.
It can be seen that the stagnation temperature rise only depends on the velocity difference between the object and the gas, and is
independent of the gas's density, temperature, or pressure. Note, however, that a lower molar mass implies a
higher specific heat, and, hence, a smaller stagnation temperature rise.



Next: Mach Number
Up: One-Dimensional Compressible Inviscid Flow
Previous: Sound Waves
Richard Fitzpatrick
2016-01-22