


Next: Decomposition of Tide Generating
Up: Terrestrial Ocean Tides
Previous: Introduction
Consider an (almost) spherical
planet of mass  , and radius
, and radius 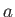 , and a spherical moon of mass
, and a spherical moon of mass  , that execute (almost) circular orbits about their mutual center of mass.
Let
, that execute (almost) circular orbits about their mutual center of mass.
Let 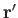 (where
(where 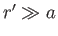 ) represent
the vector position of the center of the moon, relative to the center of the planet. It follows that
(Fitzpatrick 2012)
) represent
the vector position of the center of the moon, relative to the center of the planet. It follows that
(Fitzpatrick 2012)
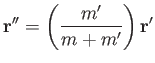 |
(12.1) |
is the vector position of the center of mass, relative to the
center of the planet.
Moreover, the planet and moon both orbit the center of mass with angular velocity 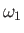 , where (Fitzpatrick 2012)
, where (Fitzpatrick 2012)
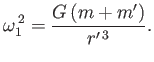 |
(12.2) |
Here, 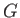 is the universal gravitational constant (Yoder 1995).
is the universal gravitational constant (Yoder 1995).
Neglecting the planet's axial rotation (which is introduced into our analysis in Section 12.6), the planet's orbital motion about the
center of mass causes its constituent points to execute circular orbits of radius 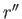 with angular velocity
with angular velocity 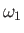 . The centers of these orbits have the same spatial relation to the center of mass that the constituent points have to the
center of the planet.
Moreover, the orbits lie in parallel planes.
Thus, the common centripetal acceleration of the constituent points is (Fitzpatrick 2012)
. The centers of these orbits have the same spatial relation to the center of mass that the constituent points have to the
center of the planet.
Moreover, the orbits lie in parallel planes.
Thus, the common centripetal acceleration of the constituent points is (Fitzpatrick 2012)
 |
(12.3) |
It follows, from the previous three equations, that
where  is a position vector relative to the center of the planet, and
is a position vector relative to the center of the planet, and
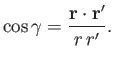 |
(12.5) |
Here,
![$\displaystyle P_n(x)=\frac{1}{2^{\,n}\,n!}\,\frac{d^{\,n}}{dx^{\,n}}\,[(x^{\,2}-1)^n],$](img4234.png) |
(12.6) |
for 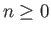 , denotes a Legendre polynomial (Abramowitz and Stegun 1965). In particular,
, denotes a Legendre polynomial (Abramowitz and Stegun 1965). In particular,
The gravitational force per unit mass exerted by the moon on one of the planet's constituent points, located at
position vector  , is written
, is written
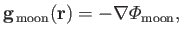 |
(12.10) |
where (Fitzpatrick 2012)
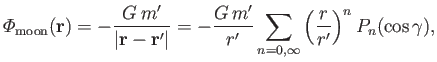 |
(12.11) |
assuming that  .
The tidal force per unit mass acting on the point (i.e., the force per unit mass that
is not compensated by the centripetal acceleration) is
.
The tidal force per unit mass acting on the point (i.e., the force per unit mass that
is not compensated by the centripetal acceleration) is
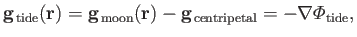 |
(12.12) |
where
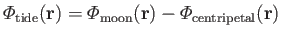 |
(12.13) |
is termed the tide generating potential.
Thus, according to Equations (12.4) and (12.11),
![$\displaystyle {\mit\Phi}_{\rm tide}({\bf r}) = - \frac{G\,m'}{r'}\left[1+\left(\frac{r}{r'}\right)^2 P_2(\cos\gamma)+ {\cal O}\left(\frac{r}{r'}\right)^3\right].$](img4246.png) |
(12.14) |
The truncation of the expansion is ultimately justified by the fact that
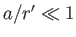 .
.



Next: Decomposition of Tide Generating
Up: Terrestrial Ocean Tides
Previous: Introduction
Richard Fitzpatrick
2016-01-22
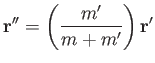
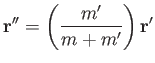
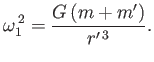
![]() with angular velocity
with angular velocity ![]() . The centers of these orbits have the same spatial relation to the center of mass that the constituent points have to the
center of the planet.
Moreover, the orbits lie in parallel planes.
Thus, the common centripetal acceleration of the constituent points is (Fitzpatrick 2012)
. The centers of these orbits have the same spatial relation to the center of mass that the constituent points have to the
center of the planet.
Moreover, the orbits lie in parallel planes.
Thus, the common centripetal acceleration of the constituent points is (Fitzpatrick 2012)
![$\displaystyle P_n(x)=\frac{1}{2^{\,n}\,n!}\,\frac{d^{\,n}}{dx^{\,n}}\,[(x^{\,2}-1)^n],$](img4234.png)
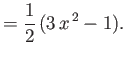
![]() , is written
, is written