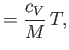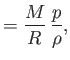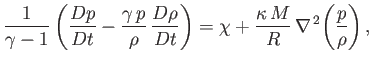Next: Dimensionless Numbers in Incompressible
Up: Mathematical Models of Fluid
Previous: Equations of Incompressible Fluid
Equations of Compressible Fluid Flow
In many situations of general interest, the flow of gases is compressible. In other words, there are significant changes in the
mass density as the gas flows from place to place. For the case of compressible flow, the continuity equation
(1.40), and the Navier-Stokes equation (1.56), must be augmented by the energy
conservation equation (1.75), as well as thermodynamic relations that specify the internal
energy per unit mass, and the temperature in terms of the density and pressure.
For an ideal gas, these relations take the form (Reif 1965)
where 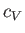 is the molar specific heat at constant volume,
is the molar specific heat at constant volume,
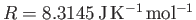 the molar ideal gas constant,
the molar ideal gas constant, 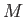 the molar mass (i.e., the mass of 1 mole of gas molecules), and
the molar mass (i.e., the mass of 1 mole of gas molecules), and  the temperature in degrees Kelvin. Incidentally, 1 mole corresponds to
the temperature in degrees Kelvin. Incidentally, 1 mole corresponds to
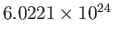 molecules. Here, we have assumed, for the sake of simplicity, that
molecules. Here, we have assumed, for the sake of simplicity, that 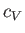 is a uniform constant.
It is also convenient to assume that the thermal conductivity,
is a uniform constant.
It is also convenient to assume that the thermal conductivity, 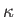 , is a
uniform constant. Making use of these approximations, Equations (1.40), (1.75), (1.83), and (1.84) can be
combined to give
, is a
uniform constant. Making use of these approximations, Equations (1.40), (1.75), (1.83), and (1.84) can be
combined to give
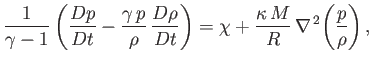 |
(1.85) |
where
 |
(1.86) |
is the ratio of the molar specific heat at constant pressure,  , to that at constant volume,
, to that at constant volume, 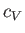 . [Incidentally, the result that
. [Incidentally, the result that 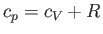 for an ideal gas is a standard theorem of thermodynamics (Reif 1965).] (See Section 14.2.) The ratio of specific heats of dry air
at
for an ideal gas is a standard theorem of thermodynamics (Reif 1965).] (See Section 14.2.) The ratio of specific heats of dry air
at
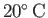 is
is  (Batchelor 2000).
(Batchelor 2000).
The complete set of equations governing compressible ideal gas flow are
where the dissipation function 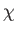 is specified in terms of
is specified in terms of  and
and  in Equation (1.74). Here,
in Equation (1.74). Here,  ,
,
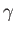 ,
, 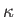 ,
, 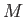 , and
, and 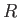 are regarded as known constants, and
are regarded as known constants, and
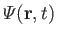 as a known function. Thus, we have five equations--namely, Equations (1.87) and (1.89), plus the three components of Equation (1.88)--for five
unknowns--namely,
the density,
as a known function. Thus, we have five equations--namely, Equations (1.87) and (1.89), plus the three components of Equation (1.88)--for five
unknowns--namely,
the density,
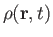 , the pressure,
, the pressure,
 , and the three components of the velocity,
, and the three components of the velocity,
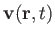 .
.



Next: Dimensionless Numbers in Incompressible
Up: Mathematical Models of Fluid
Previous: Equations of Incompressible Fluid
Richard Fitzpatrick
2016-01-22