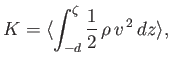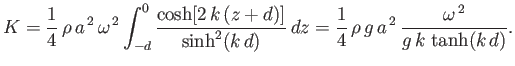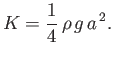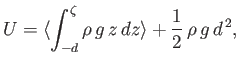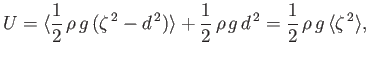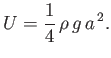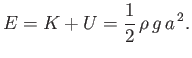Next: Wave Drag on Ships
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in Shallow
It is easily demonstrated, from the analysis contained in the previous sections, that a gravity wave of arbitrary wavenumber 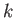 , propagating horizontally through water of depth
, propagating horizontally through water of depth 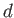 , has a phase velocity
, has a phase velocity
![$\displaystyle v_p = (g\,d)^{1/2}\left[\frac{\tanh(k\,d)}{k\,d}\right]^{1/2}.$](img3961.png) |
(11.43) |
Moreover, the ratio of the group to the phase velocity is
![$\displaystyle \frac{v_g}{v_p} =\frac{1}{2}\left[1+\frac{2\,k\,d}{\sinh(2\,k\,d)}\right].$](img3962.png) |
(11.44) |
It follows that neither the phase velocity nor the group velocity of a gravity wave can ever exceed the critical value
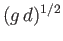 .
It is also easily demonstrated that the displacement and
velocity fields associated with a plane gravity wave of wavenumber
.
It is also easily demonstrated that the displacement and
velocity fields associated with a plane gravity wave of wavenumber
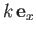 , angular frequency
, angular frequency 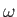 , and surface amplitude
, and surface amplitude 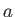 ,
are
,
are
The mean kinetic energy per unit surface area associated with a gravity wave is defined
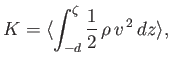 |
(11.49) |
where
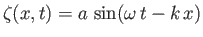 |
(11.50) |
is the vertical displacement at the surface, and
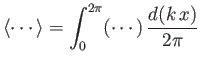 |
(11.51) |
is an average over a wavelength. Given that
 , it follows from Equations (11.47) and (11.48) that, to second order in
, it follows from Equations (11.47) and (11.48) that, to second order in 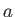 ,
,
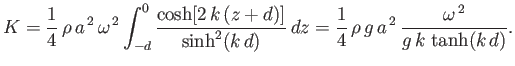 |
(11.52) |
Making use of the general dispersion relation (11.21), we obtain
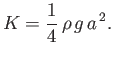 |
(11.53) |
The mean potential energy perturbation per unit surface area associated with a gravity wave is defined
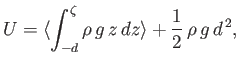 |
(11.54) |
which yields
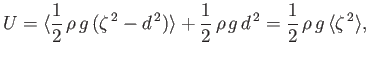 |
(11.55) |
or
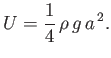 |
(11.56) |
In other words, the mean potential energy per unit surface area of a gravity wave is equal to its mean kinetic
energy per unit surface area.
Finally, the mean total energy per unit surface area associated with a gravity wave is
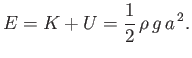 |
(11.57) |
This energy depends on the wave amplitude at the surface, but is independent of the wavelength, or the water depth.



Next: Wave Drag on Ships
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in Shallow
Richard Fitzpatrick
2016-01-22
![$\displaystyle v_p = (g\,d)^{1/2}\left[\frac{\tanh(k\,d)}{k\,d}\right]^{1/2}.$](img3961.png)