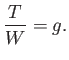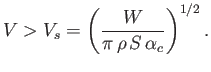Next: Exercises
Up: Incompressible Aerodynamics
Previous: Ellipsoidal Airfoils
Figure 9.14 shows a side-view schematic of a fixed wing aircraft flying in a straight-line at constant speed through stationary air. Here,  is a horizontal coordinate,
and
is a horizontal coordinate,
and  a vertical coordinate. The center of mass of the
aircraft is assumed to be moving with some fixed velocity
a vertical coordinate. The center of mass of the
aircraft is assumed to be moving with some fixed velocity  that subtends an angle
that subtends an angle 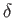 with the horizontal. Thus,
the wind velocity in the aircraft's rest frame is
with the horizontal. Thus,
the wind velocity in the aircraft's rest frame is 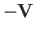 . Let the aircraft's wings, which are assumed to be parallel to
its fuselage, be inclined at an angle
. Let the aircraft's wings, which are assumed to be parallel to
its fuselage, be inclined at an angle
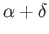 to the horizontal. It follows that
to the horizontal. It follows that 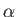 is the angle of attack. The
aircraft is subject to four forces: the thrust,
is the angle of attack. The
aircraft is subject to four forces: the thrust, 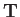 , developed by its engine, which is assumed to act parallel to its fuselage; the
lift
, developed by its engine, which is assumed to act parallel to its fuselage; the
lift 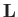 , which acts at right-angles to
, which acts at right-angles to  ; the induced drag,
; the induced drag, 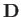 , which acts in the opposite
direction to
, which acts in the opposite
direction to  ; and the weight,
; and the weight,  , which acts vertically downward.
, which acts vertically downward.
Figure 9.14:
Side view of a fixed wing aircraft in flight.
 |
Vertical force balance yields
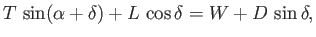 |
(9.111) |
whereas horizontal force balance gives
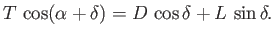 |
(9.112) |
Let us assume that the angles 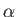 and
and 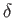 are both small.
According to Equations (9.108) and (9.109),
are both small.
According to Equations (9.108) and (9.109),
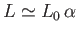 and
and
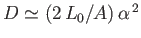 . Thus,
. Thus,
 and
and
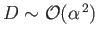 .
Moreover, it is clear from Equations (9.111) and (9.112) that
.
Moreover, it is clear from Equations (9.111) and (9.112) that
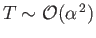 and
and
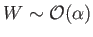 . Thus,
to lowest order in
. Thus,
to lowest order in 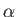 , Equation (9.111) yields
, Equation (9.111) yields
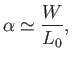 |
(9.113) |
whereas Equation (9.112) gives
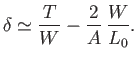 |
(9.114) |
Expression (9.113) relates the angle of attack to the ratio of the aircraft's weight to its (theoretical) maximum lift (at a given airspeed).
Expression (9.114) relates the aircraft's angle of controlled (i.e., at constant airspeed) ascent to the thrust developed by its
engine. An unpowered aircraft, such as a glider, has zero thrust. For such an aircraft, Equation (9.114) reveals that the angle of
controlled decent--which is usually termed the glide angle--takes the value
 |
(9.115) |
At fixed airspeed,  , and wing surface area,
, and wing surface area,  , (which implies that
, (which implies that 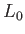 is fixed) this angle can be minimized by making the wing aspect-ratio,
is fixed) this angle can be minimized by making the wing aspect-ratio, 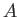 , as large as possible.
This result explains accounts for the fact that gliders (and albatrosses) have long thin wings, rather than short stubby ones. For a powered aircraft, the critical
thrust to weight ratio required to maintain level flight (i.e.,
, as large as possible.
This result explains accounts for the fact that gliders (and albatrosses) have long thin wings, rather than short stubby ones. For a powered aircraft, the critical
thrust to weight ratio required to maintain level flight (i.e., 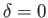 ) is
) is
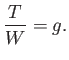 |
(9.116) |
Hence, this ratio is minimized by minimizing the glide angle, which explains why long-haul aircraft, which generally need to minimize fuel consumption,
tend to have long thin wings. Finally, as we saw in Section 9.4, if the angle of attack exceeds some (generally small) critical
value 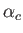 then boundary layer separation occurs on the back sides of the wings, giving rise to a greatly increased level of drag acting on the aircraft. In aerodynamics, this phenomenon
is called a stall. As is clear from Equations (9.110) and (9.113), the requirement
then boundary layer separation occurs on the back sides of the wings, giving rise to a greatly increased level of drag acting on the aircraft. In aerodynamics, this phenomenon
is called a stall. As is clear from Equations (9.110) and (9.113), the requirement
 is equivalent to
is equivalent to
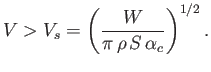 |
(9.117) |
In other words, a stall can be avoided by keeping the airspeed above the critical value 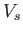 , which is known as the stall speed. Note
that the stall speed decreases with decreasing altitude, as the air becomes denser.
, which is known as the stall speed. Note
that the stall speed decreases with decreasing altitude, as the air becomes denser.



Next: Exercises
Up: Incompressible Aerodynamics
Previous: Ellipsoidal Airfoils
Richard Fitzpatrick
2016-01-22