


Next: Induced Flow
Up: Incompressible Aerodynamics
Previous: Zhukovskii's Hypothesis
Vortex Sheets
A vortex sheet is
defined as a planar array of parallel vortex filaments. Consider a uniform vortex sheet, lying in the  -
- plane, in which the
vortex filaments run parallel to the
plane, in which the
vortex filaments run parallel to the  -axis. (See Figure 9.7.) The vorticity within the sheet can be written
-axis. (See Figure 9.7.) The vorticity within the sheet can be written
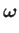 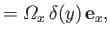 |
(9.54) |
where 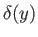 is a Dirac delta function.
Here,
is a Dirac delta function.
Here,
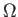
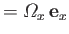 is the sheet's vortex intensity per unit length. Let
is the sheet's vortex intensity per unit length. Let
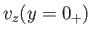 and
and
 be the
be the  -component of the fluid velocity immediately above and
below the sheet, respectively. Consider a small rectangular loop in the
-component of the fluid velocity immediately above and
below the sheet, respectively. Consider a small rectangular loop in the  -
- plane that straddles the sheet, as shown in the figure.
Integration of
plane that straddles the sheet, as shown in the figure.
Integration of
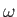
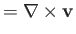 around the loop (making use of the curl theorem) yields
around the loop (making use of the curl theorem) yields
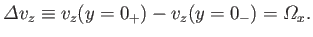 |
(9.55) |
In other words, a vortex sheet induces a discontinuity in the tangential flow across the sheet. The previous expression can easily be generalized to
give
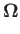  |
(9.56) |
where
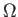 is the sheet's vortex intensity per unit length,
is the sheet's vortex intensity per unit length, 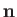 is a unit vector normal to the sheet, and
is a unit vector normal to the sheet, and
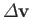 is the jump in tangential velocity across the sheet (traveling in the direction of
is the jump in tangential velocity across the sheet (traveling in the direction of 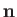 ). Furthermore, it is reasonable to assume that the previous
relation holds locally for non-planar and non-uniform vortex sheets.
). Furthermore, it is reasonable to assume that the previous
relation holds locally for non-planar and non-uniform vortex sheets.



Next: Induced Flow
Up: Incompressible Aerodynamics
Previous: Zhukovskii's Hypothesis
Richard Fitzpatrick
2016-01-22